Integrali tripli

Cosa sono gli integrali tripli?

Gli integrali tripli sono uno degli argomenti più difficili per l’esame di analisi matematica 2. La difficoltà maggiore risiede nel saper descrivere l’insieme e nel saper individuare il cambio di variabile che meglio si adatta a semplificare l’insieme di integrazione e la funzione integranda.

Gli integrali tripli sono anche detti integrali di volume, perchè geometricamente l’insieme di integrazione è costituito da un volume. La notazione che si utilizza per rappresentare gli integrali tripli è una sequenza di tre simboli di integrale consecutivi con sotto l’insieme di integrazione:

$\iiint\limits_{A}{f\left( x,y,z \right)dxdydz}$

Talvolta però si utilizza una notazione abbreviata del tipo $\int\limits_{A}{f\left( x,y,z \right)dxdydz}$

In generale gli insiemi di integrazione sono nella forma $A=\{(x,y,z) \in \mathbb{R}^3 : qualche \, condizione\}$, ovvero l’insieme dei punti (luogo geometrico dei punti) del piano cartesiano tridimensionale $\mathbb{R}^3$ che rispettano certe condizioni, che sono in generale date sotto forma di diseguaglianze.

In alcuni casi l’insieme di integrazione si riesce a rappresentarlo geometricamente e questo facilita poi la rappresentazione in altri sistemi di coordinate (polari, ellittiche o sferiche).

Significato geometrico

Per comprendere meglio cosa rappresenta un integrale triplo possiamo prendere come esempio l’integrale per il calcolo della massa di un solido. Sia A l’insieme che rappresenta il solido come un insieme di punti dello spazio, e sia $ \rho (x,y,z)$ la fuzione che descrive la densità del solido in ogni punto dello spazio (se un solido è costituito da un materiale omogeneo, la densità è una funzione costante, ma se il solido è composto da un materiale non omogeneo o da più materiali, la densità varia in ogni punto del solido). La massa di un solido può essere calcolata come:

$\iiint\limits_{A}{\rho\left( x,y,z \right)dxdydz}$

Immaginiamo di divedere il solido in infiniti piccoli parallelepipedi (volumi elementari), si ha che $dV=dxdydz$, rappresenta il volume del parallelepipedo.

Il volume elementare può essere considerato omogeneo, poichè quest’ultimo è molto piccolo. La sua massa è data dal prodotto tra il volume e la sua densità $dM=\rho dV$.  Sommando tra di loro tutte le masse elementari, si ottiene la massa del solido.

La somma di tutte le masse elementari è data dall’integrale triplo sull’insieme A (che rappresenta analiticamente il solido) della funzione densità di massa. La somma delle infinite masse elementari si rappresenta matematicamente attraverso l’integrale triplo della funzione densità di massa sull’insieme di integrazione.

Cambio di coordinate negli integrali tripli

In generale un cambio di coordinate per integrali tripli si ottiene attraverso una funzione $h:\mathbb{R}^3 \to \mathbb{R}^3$ (a volte chiamata mappa) e rappresentata da:

$ \begin{cases} x = h_1(x’, y’, z’) \\ y = h_2(x’, y’, z’) \\ z = h_3(x’, y’, z’) \end{cases}$

La matrice Jacobiana è data da:

$J=\left[\begin{matrix}   \frac{\partial {{h}_{1}}}{\partial x} & \frac{\partial {{h}_{1}}}{\partial y} & \frac{\partial {{h}_{1}}}{\partial z}  \\   \frac{\partial {{h}_{2}}}{\partial x} & \frac{\partial {{h}_{2}}}{\partial y} & \frac{\partial {{h}_{2}}}{\partial z}  \\ \frac{\partial {{h}_{3}}}{\partial x} & \frac{\partial {{h}_{3}}}{\partial y} & \frac{\partial {{h}_{3}}}{\partial z}  \\ \end{matrix}\right]$

Attraverso questa funzione è possibile passare dal sistema di coordinate $(x,y,z)$ ad un nuovo sistema di coordinate $({x}’,{y}’,{z}’)$.

Il mappaggio attraverso la funzione $h$ deve essere essere fatto sia nell’insieme $A$ che nel nuovo sistema di coordinate diventa ${A}’$, sia sulla funzione che diventa $f(x,y,z)=f(h_1, h_2, h_3)$, sia sul volume elementare che nel passare da un sistema di riferimento all’altro subisce una deformazione e se ne tiene conto attraverso il modulo del determinante della matrice Jacobiana e si ha $dxdydz=|detJ|{dx}'{dy}'{dz}’$.

Quindi nel nuovo sistema di coordinate l’integrale triplo diventa:

$\iiint\limits_{A}{f\left( x,y,z \right)dxdydz}=\iiint\limits_{{A}’} f(h_1,h_2,h_3)|detJ|{dx}'{dy}'{dz}’ $

I principali sistemi di coordinate che si utilizzano per integrali tripli sono le coordinate cilindriche e sferiche.

Coordinate cilindriche

Il passaggio in coordinate cilindriche si ottiene attraverso la funzione:

$ \begin{cases}x = \rho \cos \theta \\ y = \rho \sin \theta \\ z = z \end{cases}$

con $\rho \ge 0 $  e $\theta \in [0, 2\pi)$

Il deteminante della matrice Jacobiana per questo cambio di coordinate è dato da:

$|detJ|=\rho$

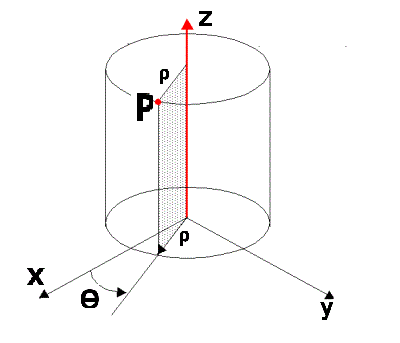
Le variabili $\rho$ e $\theta$ hanno un significato geometrico nel sistema di coordinate $(x,y,z)$

In particolare $\rho$ rappresenta la distanza del punto dall’asse z, mentre $\theta$ misura l’angolo compreso tra l’asse x e la semiretta che parte dall’origine degli assi e passante per la proiezione del punto $P$ sul piano (x,y).

Per comprendere meglio osserviamo la figura che segue.

Coordinate sferiche

Il passaggio in coordinate sferiche si ottiene attraverso la funzione:

$ \begin{cases} x = \rho \cos \theta \sin \phi \\ y = \rho \sin \theta \sin \phi \\ z = \rho \cos \phi \end{cases}$

con $\theta \in \left[ 0,2\pi  \right]$ e  $\phi \in \left[ 0,\pi  \right]$.

Il deteminante della matrice Jacobiana per questo cambio di coordinate è dato da:

$|detJ|=\rho^2 \sin \phi$

Le variabili $\rho$, $\theta$  e $\phi$ hanno un significato geometrico nel sistema di coordinate $(x,y,z)$

In particolare la variabile $\rho$ rappresenta la distanza del punto dall’origine degli assi. La variabile $\theta$ misura l’angolo compreso tra il semiasse positivo delle x e la semiretta che parte dall’origine degli assi e passante per la proiezione del punto $P$ sul piano (x,y). La variabile $\phi$ rappresenta invece l’angolo compreso tra il semiasse positivo delle z e il segmento congiungente l ‘origine degli assi al punto $P$.

Per comprendere meglio osserviamo la figura che segue.

Esercizi svolti sul calcolo dei volumi attraverso gli integrali tripli

Tutti i risultati e gli svolgimenti presenti in questa pagina, sono tutti assolutamente corretti, perché svolti e confrontati con altri professori universitari di analisi matematica dell’università di Pisa!

L’integrale triplo su un insieme che rappresenta un solido da come risultato il volume del solido.

1. Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:{{x}^{2}}+{{y}^{2}}\le \min \left[ 2-{{z}^{2}},z \right] \}$ $[\frac{8\sqrt{2}-7}{6}\pi]$  vai alla soluzione.
2. Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:{{y}^{2}}-{{x}^{2}}\le 1,\,\,\,-1\le x\le 1,\,\,\,0\le z\le 1 \}$ $[ 2\sqrt{2} + 2\ln ( \sqrt{2}+1 )]$ vai alla soluzione
3. Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:\left( x,y \right)\in T,\,\,\,0\le z\le \frac{x}{x+y}\}$ con $T$ triangolo di vertici $A=\left( 1,0 \right),B=\left( 0,1 \right),C=\left( 1,2 \right)$ $[\frac{3\ln 3}{8}]$ vai alla soluzione
4. Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:{{x}^{2}}+{{y}^{2}}\le 1,\,\,\,x\le z\le y \}$ $[\frac{2\sqrt{2}}{3}]$  vai alla soluzione
5. Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:\,\,{{x}^{2}}+{{z}^{2}}\le 1,\,\,{{y}^{2}}+{{z}^{2}}\le 1\}$ $[\frac{16}{3}]$  vai alla soluzione
6. Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:\,\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 1,\,\,y\le xz \}$ $[\frac{2}{3}\pi]$ vai alla soluzione
7. Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:\,\,{{z}^{2}}\le y\le x\le z \}$ $[\frac{1}{60}]$ vai alla soluzione
8. Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:\,\,0\le z\le 1,\,\,0\le y\le {{z}^{2}}-{{x}^{2}} \}$ $[\frac{1}{3}]$ vai alla soluzione

Soluzione esercizi sul calcolo dei volumi

1. Esercizio svolto – Calcolo del volume con il metodo della stratificazione

Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:{{x}^{2}}+{{y}^{2}}\le \min \left[ 2-{{z}^{2}},z \right] \}$ 

E inoltre la funzione $f\left( z \right)=\min \left[ 2-{{z}^{2}},z \right]$ può essere studiata graficamente:

Con riferimento alla figura si ha che $f\left( z \right)$ è rappresentato dalla curva rossa e quindi si può scrivere

$ f(z) = \left\{ \begin{array}{ll}2 – z^2 & \text{se } z < -2 \text{ o } z > 1 \\z & \text{se } -2 \leq z \leq 1\end{array} \right. $

Aggiungendo quindi la limitazione inferiore la condizione diventa $0\le {{x}^{2}}+{{y}^{2}}\le f( z)$, che fissato $z$ rappresenta l’interno di una circonferenza di raggio $\sqrt{f\left( z \right)}$ .

L’intersezione si ha soltanto nella regione in cui $f\left( z \right)>0$ quindi $z\in \left[ 0,\sqrt{2} \right]$.

L’integrale può essere calcolato per strati dove ciascuno strato è rappresentato da un cilindro di raggio $\sqrt{f\left( z \right)}$ e altezza $dz$ il cui volume è pari a $dV=\pi f\left( z \right)dz$ , per cui l’integrale diventa:

$V=\int\limits_{0}^{\sqrt{2}}{dV}=\int\limits_{0}^{\sqrt{2}}{\pi f\left( z \right)dz}=\pi \int\limits_{0}^{1}{z\,\,dz}+\pi \int\limits_{1}^{\sqrt{2}}{\left( 2-{{z}^{2}}\, \right)\,dz}=\pi \left[ \frac{{{z}^{2}}}{2} \right]_{0}^{1}+\pi \left[ 2z-\frac{{{z}^{3}}}{3} \right]_{1}^{\sqrt{2}}=\frac{8\sqrt{2}-7}{6}\pi $

2. Esercizio – calcolo volume di un solido a sezione costante – integrali tripli

Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:{{y}^{2}}-{{x}^{2}}\le 1,\,\,\,-1\le x\le 1,\,\,\,0\le z\le 1 \}$ 

Le prime due condizioni ${{y}^{2}}-{{x}^{2}}\le 1,\,\,\,-1\le x\le 1,$ descrivono la superficie compresa tra l’iperbole e le rette di equazione $x=-1$ e $x=1$ . La terza condizione $\,-1\le z\le 1$ è invece indipendente dalle altre 2. Pertanto l’insieme $E$ è un solido avente sezione costante come quella disegnata in figura e lungo l’asse z va tra -1 e 1. Quindi il volume sarà pari all’area della sezione moltiplicata per l’altezza che quindi $V=A\cdot \left( 1-0 \right)=A$

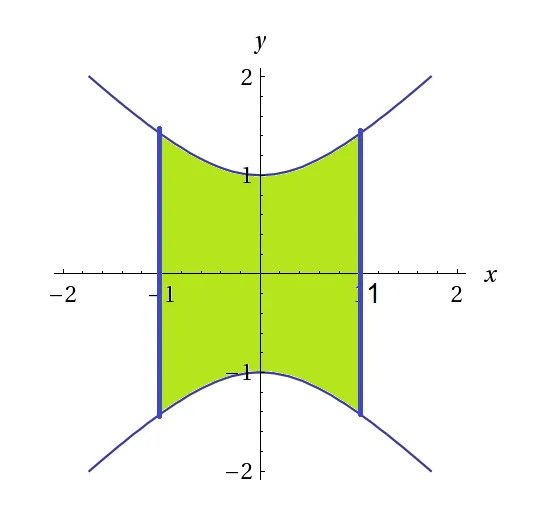
il volume è il solido che si ottiene innalzando la superficie in figura

L’area della sezione è pari a $A=\int\limits_{x=-1}^{1}{\int\limits_{y=-\sqrt{1+{{x}^{2}}}}^{\sqrt{1+{{x}^{2}}}}{\,dy}\,dx}=\int\limits_{x=-1}^{1}{2\sqrt{1+{{x}^{2}}}\,dx}=$

$= \left[ x\sqrt{x^2+1} + \ln \left( x+\sqrt{x^2+1} \right) \right]_{-1}^{1}$

$= 2\sqrt{2} + \ln \left( \frac{\sqrt{2}+1}{\sqrt{2}-1} \right)$

$= 2\sqrt{2} + \ln \left( \frac{(\sqrt{2}+1)^2}{(\sqrt{2}-1)(\sqrt{2}+1)} \right)$

$= 2\sqrt{2} + 2\ln ( \sqrt{2}+1 ) = V$

3. Esercizio volume di un solido – metodo dell’integrazione per fili

Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:\left( x,y \right)\in T,\,\,\,0\le z\le \frac{x}{x+y}\}$ con $T$ triangolo di vertici $A=\left( 1,0 \right),B=\left( 0,1 \right),C=\left( 1,2 \right)$

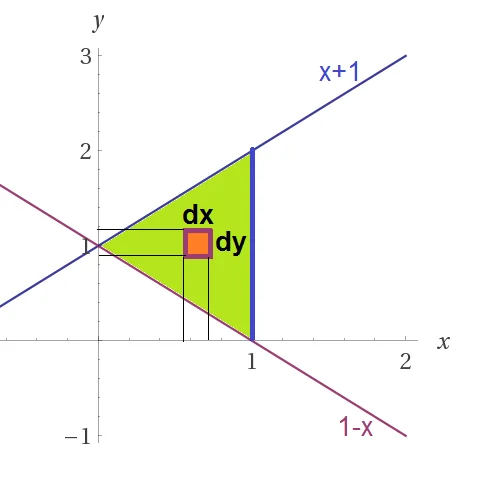
Integrazione per fili

Si può osservare che $\frac{x}{x+y}$ è una quantità sempre positiva su $T$ essendo posizionato nel quadrante in cui $x>0,y>0$ , quindi c’è intersezione tra${{f}_{1}}\left( x,y \right)=0$ e ${{f}_{2}}\left( x,y \right)=\frac{x}{x+y}$ lungo tutto il triangolo.

Il volume può essere calcolato integrando per fili, dove ciascun filo è rappresentato da un parallelepipedo di base $dx$ e $dy$ e altezza pari alla differenza tra le due funzioni tra cui è compresa la $z$ . E quindi si ha che $dV=\left[ {{f}_{2}}\left( x,y \right)-{{f}_{1}}\left( x,y \right) \right]dxdy$ e l’integrale diventa:

$V=\iint\limits_{T}{dV}=\iint\limits_{T}{\frac{x}{x+y}dxdy}=\int\limits_{x=0}^{1}{\int\limits_{y=1-x}^{1+x}{\frac{x}{x+y}dxdy}}=\int\limits_{x=0}^{1}{\left[ x\ln \left( x+y \right) \right]_{1-x}^{1+x}dx}=\int\limits_{x=0}^{1}{x\ln \left( 1+2x \right)dx}=\frac{3\ln 3}{8}$

4. Esercizio integrale triplo svolto – calcolo del Volume di un solido in coordinate polari

Calcolare il volume dell’insieme $E=\left\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:{{x}^{2}}+{{y}^{2}}\le 1,\,\,\,x\le z\le y \right\}$

In coordinate polari l’insieme diventa $0\le \rho \le 1$ , $\rho \cos \theta \le z\le \rho \sin \theta $

Bisogna verificare se ci sono limitazioni sull’angolo. Per fare ciò bisogna verificare per quali valori di $\theta \in \left[ 0,2\pi \right]$ risulta $\cos \theta <\sin \theta $ . La disuguaglianza è verificata per $\frac{\pi }{4}\le \theta \le \frac{5}{4}\pi $ .

L’integrale diventa quindi:

$\iiint\limits_{V}{dxdydz}=\int\limits_{\rho =0}^{1}{\int\limits_{\theta =\frac{\pi }{4}}^{\frac{5\pi }{4}}{\int\limits_{z=\rho \cos \theta }^{\rho \sin \theta }{\rho \,\,d\rho d\theta dz}}}=\int\limits_{\rho =0}^{1}{\int\limits_{\theta =\frac{\pi }{4}}^{\frac{5\pi }{4}}{\rho \left( \sin \theta -\cos \theta \right)\rho \,\,d\rho \,d\theta }}=$

$\left[ \frac{{{\rho }^{3}}}{3} \right]_{0}^{1}\left[ -\cos \theta -\sin \theta \right]_{\frac{\pi }{4}}^{\frac{5\pi }{4}}=\frac{2\sqrt{2}}{3}$

5. Esercizio su integrale triplo per il calcolo del volume di un insieme svolto – Volume dell’intersezione tra due cilindri

Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:\,\,{{x}^{2}}+{{z}^{2}}\le 1,\,\,{{y}^{2}}+{{z}^{2}}\le 1\}$

Si tratta del volume compreso tra due cilindri aventi come base una circonferenza di raggio unitario e come assi di simmetria rispettivamente l’asse y e l’asse x.

Invertendo le disuguaglianze si ha $-\sqrt{1-{{z}^{2}}}\le x\le \sqrt{1-{{z}^{2}}}$ e $-\sqrt{1-{{z}^{2}}}\le y\le \sqrt{1-{{z}^{2}}}$. Si osserva che tagliando il solido parallelamente rispetto al piano $z=0$, essendo $x$ e $y$ indipendenti l’uno dall’altro ed avendo entrambi le stesse limitazioni, il solido presenta una sezione quadrata. Pertanto l’integrale può essere calcolato per strati sezionandolo parallelamente al piano formato dagli assi x e y, ottenendo così volumi elementari dove la base è un quadrato di lato $2\sqrt{1-{{z}^{2}}}$ e altezza pari a $dz$, quindi $dV=A\left( z \right)dz=4\left( 1-{{z}^{2}} \right)dz$.

$V=\int\limits_{-1}^{1}{4\left( 1-{{z}^{2}} \right)dz}=\left[ z-\frac{{{z}^{3}}}{3} \right]_{-1}^{1}=8-\frac{8}{3}=\frac{16}{3}$

6. Esercizio su integrali tripli – Calcolo del Volume di un solido la cui sezione è un semicerchio

Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:\,\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 1,\,\,y\le xz \}$

Si osserva che sezionando il solido a quota z si ha che ${{x}^{2}}+{{y}^{2}}\le 1-{{z}^{2}}$ che rappresenta l’interno di una circonferenza di raggio $\sqrt{1-{{z}^{2}}}$ e $y\le xz$ che rappresenta il semipiano sottostante una retta passante per l’origine. L’intersezione tra le due regioni di piano fanno si che la sezione del solido ottenuta tagliandolo in maniera trasversale rispetto all’asse $z$sia una semicirconferenza. Il volume può essere calcolato per strati, dove ciascuno strato è costituito da un semi-cilindro di altezza $dz$ e area $A\left( z \right)=\frac{1}{2}\pi {{\left[ r\left( z \right) \right]}^{2}}=\frac{1}{2}\pi \left( 1-{{z}^{2}} \right)$ , e quindi il volume elementare è pari a $dV=\frac{1}{2}\pi \left( 1-{{z}^{2}} \right)dz$.

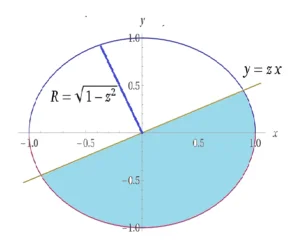
$V=\int\limits_{-1}^{1}{dV}=\int\limits_{-1}^{1}{\frac{1}{2}\pi \left( 1-{{z}^{2}} \right)dz}=\frac{1}{2}\pi \left[ z-\frac{{{z}^{3}}}{3} \right]_{-1}^{1}=\frac{2}{3}\pi $

7. Esercizio su integrale triplo per il calcolo del volume: Calcolare il volume dell’insieme

Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:\,\,{{z}^{2}}\le y\le x\le z \}$

Questo volume può essere calcolato integrando per fili.

Come superficie di base si può prendere${{z}^{2}}\le z\Rightarrow 0\le z\le 1$ e ${{z}^{2}}\le x\le z$. Ciascun filo avrà come base il rettangolo elementare di lati$dx$ e $dy$ , e si estenderà in altezza tra ${{f}_{2}}\left( x,y \right)={{z}^{2}}$e ${{f}_{1}}\left( x,y \right)=x$ cioè ${{z}^{2}}\le y\le x$ .

$ V = \iint\limits_{S}{\left( x-{{z}^{2}} \right)dxdz} = \int\limits_{z=0}^{1}{\int\limits_{x={{z}^{2}}}^{z}{dxdz}} = \int\limits_{0}^{1}{\left[ \frac{{{x}^{2}}}{2}-{{z}^{2}}x \right]_{{{z}^{2}}}^{z}dz} = \int\limits_{0}^{1}{\left( \frac{{{z}^{2}}}{2}-{{z}^{3}}+\frac{{{z}^{4}}}{2} \right)dz} = \frac{1}{60} $

8. Integrale triplo svolto – calcolo del Volume di un solido a sezione fissata

Calcolare il volume dell’insieme $E=\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}:\,\,0\le z\le 1,\,\,0\le y\le {{z}^{2}}-{{x}^{2}} \}$

Questo volume può essere calcolato per strati. Si osserva che fissato $z$ la sezione $S$ del solido è la superficie compresa tra la parabola di vertice $V=\left( 0,{{z}^{2}} \right)$ e simmetrica rispetto all’ordinata e la retta di equazione $y=0$. Il volume elementare è il solido avente sezione $S$ed area pari $A\left( z \right)$ e altezza pari a $dz$e il suo volume è dato da $dV=A\left( z \right)dz$.

superficie compresa tra l’ascissa e la parabola

Per cui $V=\int\limits_{0}^{1}{A\left( z \right)dz}$ dove $A\left( z \right)=\iint\limits_{S}{dxdy}=\int\limits_{x=-z}^{z}{\int\limits_{y=0}^{{{z}^{2}}-{{x}^{2}}}{dy\,dx}=\int\limits_{x=-z}^{z}{\left( {{z}^{2}}-{{x}^{2}} \right)dx}}=\left[ {{z}^{2}}x-\frac{{{x}^{3}}}{3} \right]_{-z}^{z}=\frac{4{{z}^{3}}}{3}$

Ed infine si ha che il volume è $V=\frac{4}{3}\int\limits_{0}^{1}{{{z}^{3}}dz}=\left[ \frac{{{z}^{4}}}{3} \right]_{0}^{1}=\frac{1}{3}$

Esercizi svolti su integrali tripli

Calcolare il valore dei seguenti integrali tripli:

1. $\iiint\limits_{A}{\frac{y}{{{z}^{4}}+1}dxdydz} $, $A=\{(x,y,z)\in {{\mathbb{R}}^{3}}:\,\,\,0\le z\le 1,\,\,\,\,{{x}^{2}}+{{y}^{2}}\le {{z}^{2}},\,\,\,\,z\le x+y \}$ $[\frac{\ln 2}{24}]$ Vai alla soluzione
2. $\iiint\limits_{A}{{{( y+z )}^{2}}dxdydz} $, $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,\,{{y}^{2}}+{{z}^{2}}\le 25,\,\,\,\,z\le x+4,\,\,x\le 1 \}$ $[\frac{3125}{2}\pi]$  Vai alla soluzione
3. $\iiint\limits_{A}{( x+{{z}^{3}}\sin {{y}^{2}} )dxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,\,2x\le {{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 1,\,x\ge 0 \}$ $[\frac{\pi }{24}]$ Vai alla soluzione
4. $\iiint\limits_{A}{zdxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,\,|x-z|+|y-z|\le 1+z,\,\,\,\,0\le z\le 1 \}$  $[\frac{17}{6}]$ Vai alla soluzione
5. $\iiint\limits_{A}{\frac{1}{{{z}^{3}}}dxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,0\le z\le 1\,\,,\,\,{{x}^{2}}+{{y}^{2}}\le 5{{z}^{2}},\,\,\frac{1}{4}\le {{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 1\,\,\, \}$  $[5\pi \log 2]$ Vai alla soluzione, Seguendo questo link troverai una soluzione dello stesso integrale in coordinate polari (molto più lunga e calcolosa, ma utile per comprendere che spesso i calcoli possono essere fatti in maniera diversa e si arriva esattamente allo stesso risultato, e quindi è importante anche ragionare su quale può essere la strada più efficace che ci porta al risultato con il minor sforzo).
6. $\iiint\limits_{A}{xzdxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,\,,{{x}^{2}}+{{y}^{2}}\le 1,\,\,x\ge 0,y\ge 0\,\,,-1\le z\le 0\, \} [-\frac{1}{6}]$ Vai alla soluzione
7. $\iiint\limits_{A}{\frac{1}{{{z}^{3}}}dxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,z\ge \sqrt{3{{x}^{2}}+3{{y}^{2}}},\,\frac{1}{4}\le {{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 1\, \}$ $[\frac{\pi \log 2}{3}]$ Vai alla soluzione
8. $\iiint\limits_{A}{|x|dxdydz}$ ,  $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,{{y}^{2}}+{{z}^{2}}\le 1,z\ge {{x}^{2}}\, \}$, $[\frac{2}{3}]$ Vai alla soluzione
9. $\iiint\limits_{A}{\frac{x}{{{( y-1)}^{2}}}dxdydz}$,$A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,{{x}^{2}}+{{y}^{2}}-2y\le 0,x\ge 0,0\le z\le y\le \frac{1}{2}\,\}$  $[\frac{7}{16}-\frac{1}{2}\log 2]$Vai alla soluzione
10. $\iiint\limits_{A}{\frac{1}{\sqrt{{{x}^{2}}+{{y}^{2}}}}dxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,z\ge 0,{{x}^{2}}+{{y}^{2}}\le {{z}^{2}},{{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 1\, \}$ $[\frac{{{\pi }^{2}}}{4}]$  Vai alla soluzione
11. $\iiint\limits_{A}{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}dxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,{{x}^{2}}+{{y}^{2}}\le {{z}^{2}},-1\le z\le 2 \}$  $[\frac{99}{100}\pi] $  Vai alla soluzione
12. $\iiint\limits_{A}{| {{x}^{2}}-{{y}^{2}} |dxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,0\le z\le 2-\sqrt{{{x}^{2}}+{{y}^{2}}} \}$  $[\frac{32}{5}]$ Vai alla soluzione
13. $\iiint\limits_{A}{zdxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,2{{x}^{2}}-1\le z\le {{x}^{2}}-{{y}^{2}} \}$ $[-\frac{\pi }{6}]$ Vai alla soluzione
14. $\iiint\limits_{A}{( 1+xy )dxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,{{z}^{2}}+1\le {{x}^{2}}+{{y}^{2}}\le z+3 \}$ Vai alla soluzione

Qui puoi trovare altri 6 ESERCIZI SVOLTI sul calcolo di integrali tripli, utilissimi per prepararti all’esame di analisi matematica.

Lezioni di Analisi Matematica 2