Indice dei contenuti
Calcolare il seguente integrale triplo:
$\iiint\limits_{A}{\frac{1}{{{z}^{3}}}dxdydz}$ ,
$ A = \{ 0 \leq z \leq 1, \quad x^2 + y^2 \leq 5z^2, \quad \frac{1}{4} \leq x^2 + y^2 + z^2 \leq 1 \} $
Si tratta di Integrale triplo su intersezione tra due sfere e cono, perché graficando geometricamente l’insieme di integrazione e visualizzandolo in tre dimensioni, vediamo proprio l’intersezione tra un cono e due sfere. Tutto suggerisce di svolgerlo in coordinate sferiche, visto che l’insieme di integrazione ha una simmetria sferica, ma in questo caso, anche se non è il metodo consigliato proveremo a risolverlo in coordinate polari.
I risultati sono tutti assolutamente corretti, perché confrontati con altri professori universitari di analisi matematica!
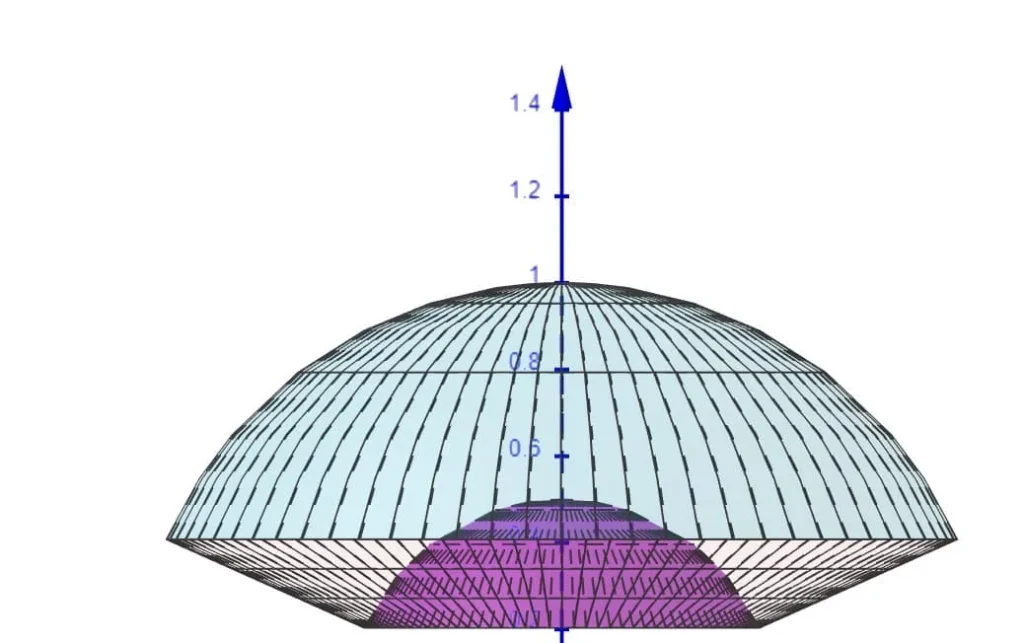
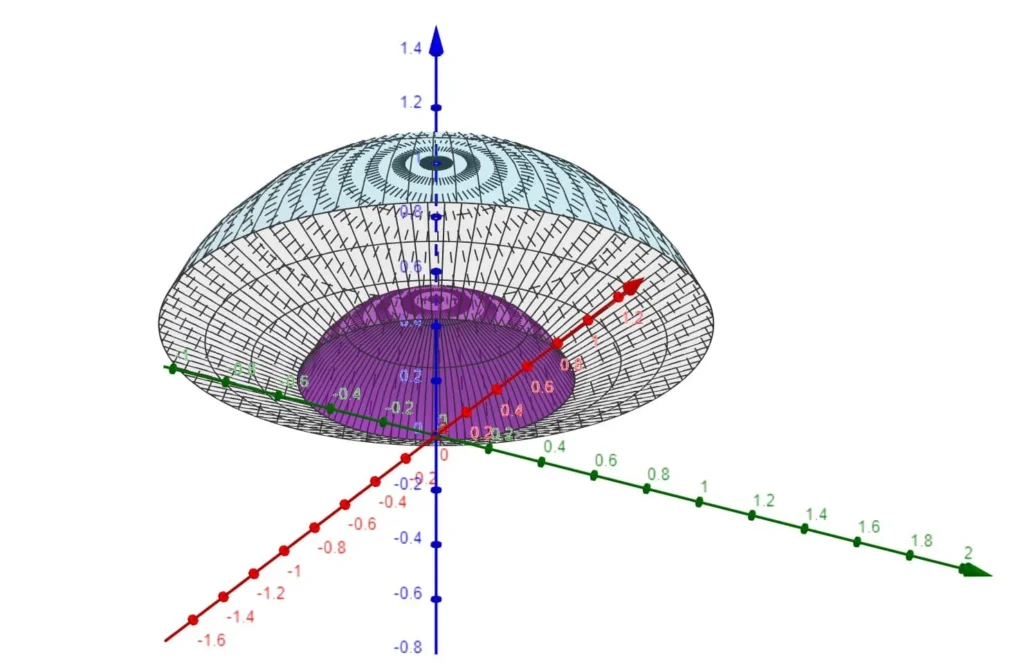
Rappresentazione dell’insieme di integrazione (intersezione tra due sfere e cono)
Per prima cosa proviamo a capire di cosa si tratta l’insieme di integrazione.
La disequazione${{x}^{2}}+{{y}^{2}}\le 5{{z}^{2}}$ rappresenta la parte interna di un cono. La disequazione$\,\frac{1}{4}\le {{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 1$ rappresenta il volume compreso tra due sfere concentriche di centro nell’origine e raggi pari rispettivamente a Ra=1/2 e Rb=1.
Calcolo del risultato dell’integrale triplo
$ A = \{ 0 \leq z \leq 1, \quad x^2 + y^2 \leq 5z^2, \quad \frac{1}{4} \leq x^2 + y^2 + z^2 \leq 1 \} $
Comunque si fissa z, si ha che la sezione del solido è la superficie compresa tra due circonferenze. Per capire quali tra quali valori prendere il raggio del cerchio interno e del cerchio esterno possiamo provare a graficare le funzioni ${{f}_{1}}\left( z \right)=5{{z}^{2}}$, ${{f}_{2}}\left( z \right)=1-{{z}^{2}}$ e ${{f}_{3}}\left( z \right)=\frac{1}{4}-{{z}^{2}}$ calcolando le varie intersezioni.
Si ha che $5{{z}^{2}}\ge \frac{1}{4}-{{z}^{2}}$ $\Rightarrow $ $6{{z}^{2}}\ge \frac{1}{4}$ $\Rightarrow $ $z\ge \frac{1}{2\sqrt{6}}$
Possiamo riscrivere l’insieme A, nella seguente forma:
$ A = \{ \frac{1}{2\sqrt{6}} \leq z \leq 1, \quad \max \{0,\frac{1}{4}-z^2\} \leq x^2+y^2 \leq \min \{1-z^2,5z^2\} \} $
A questo punto calcoliamo le altre disequazioni:
$\frac{1}{4}-{{z}^{2}}\ge 0\,$ $\Rightarrow $ ${{z}^{2}}\le \frac{1}{4}$ $\Rightarrow $ $\frac{1}{2\sqrt{6}}\le z\le \frac{1}{2}$
$1-{{z}^{2}}\le 5{{z}^{2}}$ $\Rightarrow $ $6{{z}^{2}}\ge 1$ $\Rightarrow $ $z\ge \frac{1}{\sqrt{6}}$
E per concludere possiamo scrivere:
Per la funzione minimo:
$ \min \{1-z^2, 5z^2\} = \begin{cases} 1-z^2, & z \geq \frac{1}{\sqrt{6}} \\ 5z^2, & \frac{1}{2\sqrt{6}} \leq z < \frac{1}{\sqrt{6}} \end{cases} $
Per la funzione massimo:
$ \max \left\{\frac{1}{4}-z^2, 0\right\} = \begin{cases} 0, & z \geq \frac{1}{2} \\ \frac{1}{4}-z^2, & \frac{1}{2\sqrt{6}} \leq z < \frac{1}{2} \end{cases} $
Passaggio in coordinate cilindriche
Le equazioni che esprimono le coordinate cilindriche nello spazio sono:
$\left\{\begin{aligned}x &= \rho \cos \theta \\y &= \rho \sin \theta \\z &= z\end{aligned}\right.$
dove $\rho$ rappresenta la distanza radiale del punto dall’asse $z$, $\theta$ è l’angolo azimutale misurato dal semiasse positivo $x$ nel piano $xy$, e $z$ è l’altezza del punto lungo l’asse $z$.
In coordinate cilindriche l’insieme diventa l’unione di tre sottoinsiemi:
${A}’=\{ \frac{1}{2\sqrt{6}}\le z\le \frac{1}{\sqrt{6}},\,\,0\le \theta \le 2\pi ,\,\,\sqrt{\frac{1}{4}-{{z}^{2}}}\le \rho \le \sqrt{5}z\, \}\cup$
$\{ \frac{1}{\sqrt{6}}\le z\le \frac{1}{2},\,\,0\le \theta \le 2\pi ,\,\,\sqrt{\frac{1}{4}-{{z}^{2}}}\le \rho \le \,\sqrt{1-{{z}^{2}}} \}\cup$
$\{ \frac{1}{2}\le z\le 1,\,\,0\le \theta \le 2\pi ,\,\,0\le \rho \le \,\sqrt{1-{{z}^{2}}}\}$
A questo punto torniamo all’integrale triplo, facciamo il cambio di coordinate ricordando di moltiplicare per il valore assoluto del determinante della matrice Jacobiana e spezziamolo nella somma di tre integrali.
$\iiint\limits_{A}{\frac{1}{{{z}^{3}}}dxdydz}=\iiint\limits_{{A’}} \frac{1}{z^3} \rho \, d\rho \, d\theta \, dz$
$\int\limits_{z=1/(2\sqrt{6})}^{1/\sqrt{6}}{\int\limits_{\theta =0}^{2\pi }{\int\limits_{\rho =\sqrt{\frac{1}{4}-{{z}^{2}}}}^{\sqrt{5{{z}^{2}}}}{\frac{1}{{{z}^{3}}}\rho d\rho d\theta dz}}}+\int\limits_{z=1/\sqrt{6}}^{1/2}{\int\limits_{\theta =0}^{2\pi }{\int\limits_{\rho =\sqrt{\frac{1}{4}-{{z}^{2}}}}^{\sqrt{1-{{z}^{2}}}}{\frac{1}{{{z}^{3}}}\rho d\rho d\theta dz}}}+\int\limits_{z=1/2}^{1}{\int\limits_{\theta =0}^{2\pi }{\int\limits_{\rho =0}^{\sqrt{1-{{z}^{2}}}}{\frac{1}{{{z}^{3}}}\rho d\rho d\theta dz}}}=$
$2\pi [ \int\limits_{z=1/(2\sqrt{6})}^{1/\sqrt{6}}{\frac{1}{{{z}^{3}}}\int\limits_{\rho =\sqrt{\frac{1}{4}-{{z}^{2}}}}^{\sqrt{5{{z}^{2}}}}{\rho d\rho dz}}+\int\limits_{z=1/\sqrt{6}}^{1/2}{\frac{1}{{{z}^{3}}}\int\limits_{\rho =\sqrt{\frac{1}{4}-{{z}^{2}}}}^{\sqrt{1-{{z}^{2}}}}{\rho d\rho dz}}+\int\limits_{z=1/2}^{1}{\frac{1}{{{z}^{3}}}\int\limits_{\rho =0}^{\sqrt{1-{{z}^{2}}}}{\rho d\rho dz}} ]=$
$2\pi [ \int\limits_{z=1/(2\sqrt{6})}^{1/\sqrt{6}}{\frac{1}{{{z}^{3}}}\left[ \frac{{{\rho }^{2}}}{2} \right]_{\sqrt{\frac{1}{4}-{{z}^{2}}}}^{\sqrt{5{{z}^{2}}}}dz}+\int\limits_{z=1/\sqrt{6}}^{1/2}{\frac{1}{{{z}^{3}}}\left[ \frac{{{\rho }^{2}}}{2} \right]_{\sqrt{\frac{1}{4}-{{z}^{2}}}}^{\sqrt{1-{{z}^{2}}}}}+\int\limits_{z=1/2}^{1}{\frac{1}{{{z}^{3}}}\left[ \frac{{{\rho }^{2}}}{2} \right]_{0}^{\sqrt{1-{{z}^{2}}}}} ]=$
$\pi [ \int\limits_{z=1/(2\sqrt{6})}^{1/\sqrt{6}}{\frac{1}{{{z}^{3}}}\left[ \left( 5{{z}^{2}} \right)-\left( \frac{1}{4}-{{z}^{2}} \right) \right]dz}+\int\limits_{z=1/\sqrt{6}}^{1/2}{\frac{1}{{{z}^{3}}}\left[ \left( 1-{{z}^{2}} \right)-\left( \frac{1}{4}-{{z}^{2}} \right) \right]dz}+\int\limits_{z=1/2}^{1}{\frac{1}{{{z}^{3}}}\left( 1-{{z}^{2}} \right)dz}]=$
Ora abbiamo la somma di tre integrali nella sola variabile z. Andiamo a calcolare gli integrali uno alla volta e poi alla fine facciamo la somma.
$\int\limits_{z=1/(2\sqrt{6})}^{1/\sqrt{6}}{\frac{1}{{{z}^{3}}}\left[ \left( 5{{z}^{2}} \right)-\left( \frac{1}{4}-{{z}^{2}} \right) \right]dz}\,=$ $\int\limits_{z=1/(2\sqrt{6})}^{1/\sqrt{6}}{\frac{6}{z}-\frac{1}{4{{z}^{3}}}\,dz}=6\log 2-\frac{9}{4}$
$\int\limits_{z=1/\sqrt{6}}^{1/2}{\frac{1}{{{z}^{3}}}\left[ \left( 1-{{z}^{2}} \right)-\left( \frac{1}{4}-{{z}^{2}} \right) \right]dz}=$ $\int\limits_{z=1/\sqrt{6}}^{1/2}{\frac{3}{4{{z}^{3}}}dz}=\frac{3}{4}$
$\int\limits_{z=1/2}^{1}{\frac{1}{{{z}^{3}}}\left( 1-{{z}^{2}} \right)dz}=$ $\int\limits_{z=1/2}^{1}{\frac{1}{{{z}^{3}}}-\frac{1}{z}dz}=\frac{3}{2}-\log 2$
Per finire torniamo all’integrale principale e sommiamo tutto:
$\otimes =\pi \left( 6\log 2-\frac{9}{4}+\frac{3}{4}+\frac{3}{2}-\log 2 \right)=$ $5\pi \log 2$
Finalmente siamo arrivati alla soluzione dell’integrale che vale $5\pi \log 2$ .
Abbiamo concluso l’ integrale triplo svolto su intersezione tra due sfere e cono. Questo esercizio è un esempio di integrale triplo di difficoltà elevata e molto contoso. Continua la navigazione sul sito per provare altri esempi.
Approfondimento sulla parametrizzazione delle superfici in R³
Un esercizio molto utile per imparare a parametrizzare superfici è quello di provare a parametrizzare la superficie esterna del solido rappresentato dall’insieme A.
Una possibile soluzione è:
${{\Sigma }_{1}}=\left( \rho \cos \theta ,\rho \sin \theta ,\frac{\rho }{\sqrt{5}} \right)$ , $\frac{\sqrt{5}}{2\sqrt{6}}\le \rho \le \frac{\sqrt{5}}{\sqrt{6}}$ , $0\le \theta \le 2\pi $ (rappresenta la superficie del tronco di cono)
${{\Sigma }_{2}}=\left( \cos \theta \sin \phi ,\sin \theta \sin \phi ,\cos \phi \right)$, $0\le \theta \le 2\pi $, $0\le \phi \le {{\cos }^{-1}}\left( \frac{1}{\sqrt{6}} \right)$ (rappresenta la superficie della calotta sferica di raggio 1)
${{\Sigma }_{3}}=\left( \frac{1}{2}\cos \theta \sin \phi ,\frac{1}{2}\sin \theta \sin \phi ,\frac{1}{2}\cos \phi \right)$, $0\le \theta \le 2\pi $, $0\le \phi \le {{\cos }^{-1}}\left( \frac{1}{\sqrt{6}} \right)$ (rappresenta la superficie della calotta sferica di raggio 1/2)
Un’altra possibile soluzione è
${{\Sigma }_{1}}=\left( \rho \cos \theta ,\rho \sin \theta ,\frac{\rho }{\sqrt{5}} \right)$ , $\frac{\sqrt{5}}{2\sqrt{6}}\le \rho \le \frac{\sqrt{5}}{\sqrt{6}}$ , $0\le \theta \le 2\pi $ (rappresenta la superficie del tronco di cono)
${{\Sigma }_{2}}=\left( \rho \cos \theta ,\rho \sin \theta ,\sqrt{1-{{\rho }^{2}}} \right)$, $0\le \rho \le \frac{\sqrt{5}}{\sqrt{6}}$, $0\le \phi \le {{\cos }^{-1}}\left( \frac{1}{\sqrt{6}} \right)$ (rappresenta la superficie della calotta sferica di raggio 1)
${{\Sigma }_{3}}=\left( \rho \cos \theta ,\rho \sin \theta ,\sqrt{\frac{1}{4}-{{\rho }^{2}}} \right)$, $0\le \rho \le \frac{\sqrt{5}}{2\sqrt{6}}$, $0\le \phi \le {{\cos }^{-1}}\left( \frac{1}{\sqrt{6}} \right)$ (rappresenta la superficie della calotta sferica di raggio 1/2)
Stesso esercizio risvolto in coordinate sferiche (soluzione consigliata).
Lezioni di Analisi Matematica 2