Indice dei contenuti
Vogliamo studiare la continuità e la derivabilità della funzione \(f\left( x,y \right)\) nell’origine.
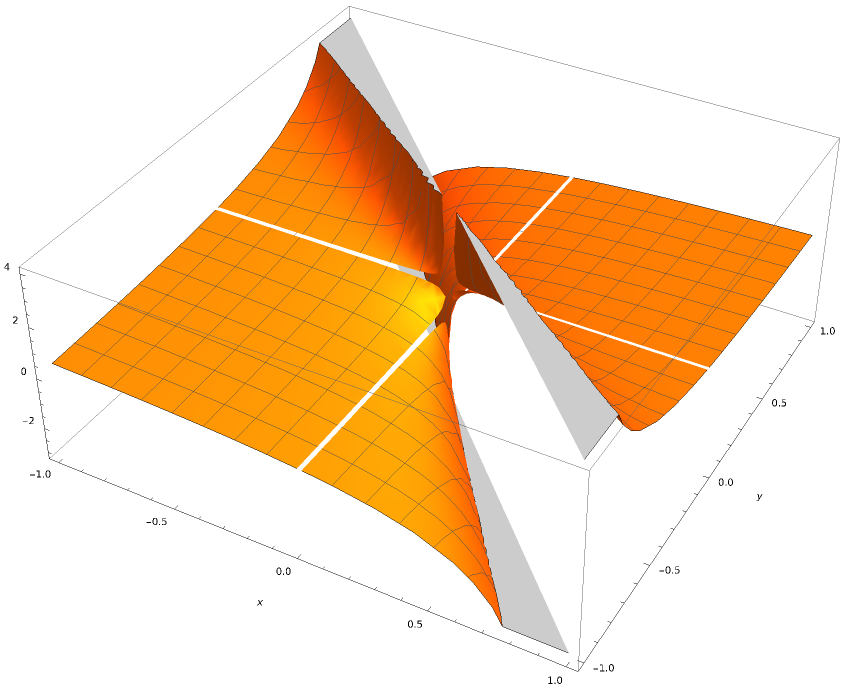
\[ f(x, y) = \begin{cases} \frac{x}{x + y} & \text{se } (x, y) \neq (0, 0) \\ 0 & \text{se } (x, y) = (0, 0) \end{cases} \]
Studio della derivabilità della funzione
Iniziamo studiando la derivabilità nell’origine della funzione\(f\left( x,y \right)\).Per fare ciò calcoliamo le due derivate parziali (rispetto all’asse x e rispetto all’asse y) attraverso la definizione, ovvero mediante il limite del rapporto incrementale.
\({{{f}’}_{x}}\left( 0,0 \right)=\underset{t\to 0}{\mathop{\lim }}\,\frac{f(t,0)-f(0,0)}{t}=\) \(\underset{t\to 0}{\mathop{\lim }}\,\frac{0}{t}=0\)
Nota bene che nel limite non si ha una forma indeterminata $\frac{0}{0}$ come si potrebbe pensare erroneamente, perché il numeratore vale esattamente 0, mentre il denominatore tende a 0.
\({{{f}’}_{y}}\left( 0,0 \right)=\underset{t\to 0}{\mathop{\lim }}\,\frac{f(0,t)-f(0,0)}{t}=\) \(\underset{t\to 0}{\mathop{\lim }}\,\frac{0}{t}=0\)
Entrambe le derivate parziali esistono e sono finite e valgono \({{{f}’}_{x}}\left( 0,0 \right)={{{f}’}_{y}}\left( 0,0 \right)=0\). Possiamo quindi concludere che la funzione\(f\left( x,y \right)\) è derivabile nell’origine.
Studio della continuità
Verifichiamo ora se la funzione è anche continua nell’origine, e per fare ciò dobbiamo verificare l’uguaglianza \(\underset{(x,y)\to (0,0)}{\mathop{\lim }}\,f\left( x,y \right)=f(0,0)\) .
Il valore della funzione nell’origine è \(f(0,0)=0\), quindi calcolando il limite della funzione nell’origine si dovrebbe avere che quest’ultimo vale zero.
Verifichiamo quindi se il limite esiste e se vale zero.
Guardando la funzione si può osservare che il numeratore e il denominatore sono dello stesso ordine di grandezza e questo ci può far pensare che sono confrontabili. Proviamo a mettere in relazione le variabili x e y.
Se poniamo ad esempio \(x=y\) il limite diventa \(\underset{x\to 0} {\mathop{\lim }}\,\frac{|x|}{x+x}\neq 0\)
La funzione non tende a zero, quindi possiamo concludere che il limite non esiste.
Deduzione: si tratta di una funzione derivabile ma non continua!!
Dal momento che una funzione derivabile in più variabili potrebbe non essere continua, è importante considerare le differenze rispetto alle funzioni con una sola variabile. Mentre nel caso delle funzioni con una sola variabile la derivata implica automaticamente la continuità, nella situazione delle funzioni in più variabili questo non è sempre vero. Questo fenomeno può essere dovuto alla complessità aggiuntiva introdotta dalla presenza di più variabili, che può rendere più difficile garantire la continuità della funzione.
Inoltre, le funzioni in più variabili presentano anche la complicazione aggiuntiva della possibilità di avere derivate parziali. Queste derivate parziali misurano il tasso di variazione della funzione rispetto a una singola variabile, mantenendo costanti le altre variabili. La presenza di derivate parziali aggiunge ulteriori sfide nella comprensione e nell’analisi delle funzioni in più variabili, e può influenzare la loro natura continua o discontinua.
Infine, vale la pena notare che l’importanza della continuità delle funzioni in più variabili risiede nella sua relazione con concetti fondamentali come la differenziabilità e la derivabilità. La continuità è un requisito essenziale per la differenziabilità delle funzioni in più variabili, quindi comprendere le relazioni tra queste proprietà è cruciale per lo studio e l’applicazione della matematica in contesti più complessi. In definitiva, l’esempio evidenzia le sfide e le peculiarità delle funzioni derivabili in più variabili, sottolineando l’importanza di approfondire la comprensione di tali concetti per una corretta analisi matematica.
L’esempio fornito dimostra chiaramente che la derivabilità di una funzione non implica necessariamente la sua continuità. Questo concetto è fondamentale nell’ambito del calcolo differenziale, poiché dimostra che esistono funzioni che possono essere derivabili in un punto senza essere continue in quel punto. In altre parole, la derivabilità di una funzione non garantisce la sua continuità in quel punto specifico.
Nel contesto delle funzioni di più variabili, la condizione sufficiente per la continuità di una funzione diventa la differenziabilità. Questo significa che se una funzione di più variabili è differenziabile in un punto, allora è anche continua in quel punto. La differenziabilità di una funzione di più variabili implica la sua continuità, rendendo questo concetto cruciale nell’analisi matematica.
In conclusione, mentre la derivabilità di una funzione non implica la sua continuità in un punto, nella teoria delle funzioni di più variabili la differenziabilità diventa una condizione sufficiente per garantire la continuità. Questi concetti sono fondamentali per comprendere il comportamento delle funzioni e le relazioni tra derivabilità e continuità in diversi contesti matematici.
In più di una variabile vale il teorema che afferma che se una funzione è differenziabile allora è anche continua´