Gli integrali tripli rappresentano uno degli strumenti matematici più potenti e versatili a disposizione di studenti, ingegneri e scienziati. Attraverso il loro studio e applicazione, possiamo esplorare e risolvere problemi complessi che riguardano il calcolo di volumi, masse, centri di massa, e molte altre proprietà fisiche di corpi nello spazio tridimensionale. Questa pagina è dedicata alla presentazione e alla soluzione di una serie di esercizi su integrali tripli, ciascuno dei quali è stato attentamente selezionato per illustrare l’applicazione di questi concetti matematici in varie situazioni.

Attraverso l’analisi dettagliata di ciascun esercizio, si mira a fornire una comprensione approfondita delle tecniche di integrazione in tre dimensioni, della scelta degli intervalli di integrazione e delle coordinate più adatte al problema (cartesiane, cilindriche o sferiche). Inoltre, si enfatizza l’importanza di interpretare correttamente i risultati in termini fisici e geometrici, fornendo una base solida per applicazioni future in contesti accademici o professionali.

Ciascun esercizio è accompagnato da una spiegazione passo-passo dei metodi risolutivi utilizzati, illustrando non solo come applicare le tecniche di integrazione tripla, ma anche come approcciarsi in modo critico e analitico ai problemi. Questo approccio non solo facilita l’apprendimento e la comprensione dei concetti fondamentali, ma stimola anche la capacità di affrontare questioni complesse con creatività e precisione.

Che tu sia uno studente alle prese con il calcolo integrale per la prima volta, un ingegnere alla ricerca di una soluzione elegante a un problema di progettazione, o semplicemente un appassionato di matematica curioso di esplorare le applicazioni tridimensionali dell’integrazione, questa pagina offre una risorsa preziosa e stimolante per il tuo viaggio nel mondo degli integrali tripli.

Tutti i risultati e gli svolgimenti presenti in questa pagina, sono tutti assolutamente corretti, perché svolti e confrontati con altri professori universitari di analisi matematica dell’università di Pisa!

Esercizi sugli integrali tripli

Esercizio 1 – Calcolo di integrale triplo

Calcolare \(\int\limits_{C}{z\,dx\,dy\,dz}\,\,\) con $C$ rappresentato da \( \sqrt{x^2 + y^2} – 1 \leq z \leq \sqrt{1 – (x^2 + y^2)} \)

Soluzione

Si tratta del volume compreso tra un cono avente come base la circonferenza che poggia sul piano x,y di raggio unitario e centrata nell’origine e una semisfera di raggio unitario anch’essa centrata nell’origine e adagiata sul piano x,y (cono gelato con un gusto solo).

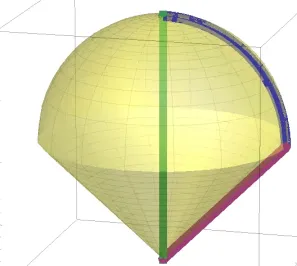
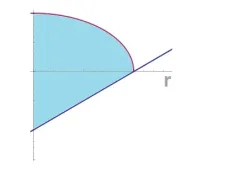
Proviamo a passare in coordinate cilindriche.\(\left( x,y,z \right)=\left( \rho \cos \theta ,\rho \sin \theta ,z \right)\), si ha che \(0\le \rho \le 1,\,\,0\le \theta \le 2\pi \) e che \(\rho -1\le z\le \sqrt{1-{{\rho }^{2}}}\)

\(\int\limits_{C}{z\,dx\,dy\,dz}\,\,=\int\limits_{\theta =0}^{2\pi }{\int\limits_{\rho =0}^{1}{\int\limits_{z=\rho -1}^{\,\sqrt{1-{{\rho }^{2}}}}{z\rho \,d\rho dz\,d\theta }}}=2\pi \int\limits_{0}^{1}{\rho \left[ \frac{{{z}^{2}}}{2} \right]}_{z=\rho -1}^{\sqrt{1-{{\rho }^{2}}}}d\rho =2\pi \int\limits_{0}^{1}{\left( \rho \frac{1-{{\rho }^{2}}}{2}-\rho \frac{1+{{\rho }^{2}}-2\rho }{2} \right)\,}d\rho =\)

\(2\pi \int\limits_{0}^{1}{{{\rho }^{2}}-{{\rho }^{3}}\,}d\rho =\frac{\pi }{6}\)

Esercizio 2 – Calcolo di integrale triplo

Calcolare il seguente integrale \(\int\limits_{C}{{{z}^{-3}}\,dx\,dy\,dz}\,\,\) con C definito dalle equazioni \({{x}^{2}}\le y\le 1\) e \(0\le z-1\le y\)

Soluzione

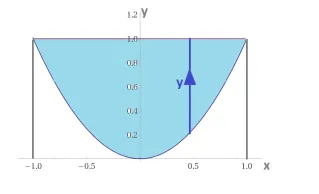
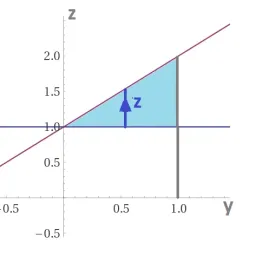
L’insieme \(C\) rappresenta l’intersezione tra un prisma a sezione triangolare ed un prisma a sezione parabolica. Ragionare sul solido generato è piuttosto complicato come d’altronde lo è provare a disegnarlo. E’ piuttosto agevole invece integrare per fili. Si osserva che le condizioni \({{x}^{2}}\le y\le 1\) e \(0\le z-1\le y\) dipendono entrambe da \(y\).

\(x\) è una quantità che varia tra \(-1\) e \(1\), visto che \({{x}^{2}}\le y\le 1\,\,\Rightarrow=\)\( \,\,{{x}^{2}}\le 1\,\,\Rightarrow\)\( -1\le x\le -1\).

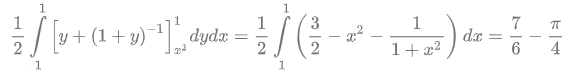
Esercizio 3 – Calcolo di integrale triplo

Calcolare \(\int\limits_{C}{\left( {{y}^{3}}+{{z}^{2}} \right)\,dx\,dy\,dz}\,\)con $C$ rappresentato dalle equazioni ${x}^{2}+{y}^{2} \le {z}^{2}$ e $1 \le z \le 2$

Soluzione

Si osserva che prendendo il solido rappresentato dall’insieme \(C\) e sezionandolo a quota \(z\) si ha una circonferenza  di centro \(\left( z,0,z \right)\) e raggio \(z\).

E’ possibile passare in coordinate cilindriche traslate \(\left( x,y,z \right)=\left(\rho \cos \theta +z,\rho \sin \theta ,z \right)\)

Il determinante della matrice Jacobiana è \(\det \left| \begin{matrix}\cos \theta& \sin \theta \, & 0 \\-\rho \sin \theta & \rho \cos \theta & 0 \\0 & 0 & 1 \\\end{matrix} \right|=\rho \)

L’integrale risulta 

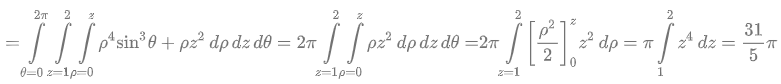
Dove si è tenuto conto del fatto che \(\int\limits_{0}^{2\pi }{{{\sin }^{3}}\theta }\,d\theta =0\) perché è l’integrale di una funzione dispari e periodica su un periodo.

Esercizio 4 – Calcolo di integrale triplo

Calcolare \(\int\limits_{C}{xy\,dx\,dy\,dz}\,\) con $C$ definito da $0 \le y \le x$, e ${x}^{2}+{y}^{2} \le 1$

Soluzione

L’insieme descritto da \(C\) è uno spicco di cilindro limitato dai piani \(y=0\) e \(y=x\). Pertanto è possibile descriverlo in coordinate sferiche .

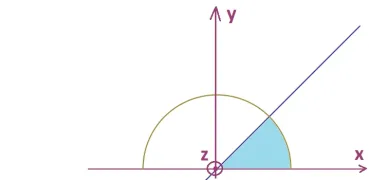
\(0\le y\le x\,\,\,\,\Rightarrow \,\,\,0\le \theta \le \frac{\pi }{4}\)

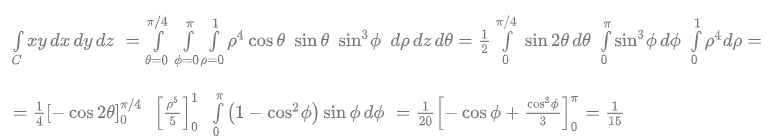
Esercizio 5- Calcolo di integrale triplo

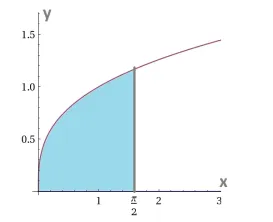
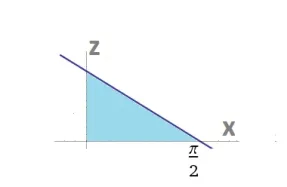
Calcolare \(\int\limits_{C}{{{y}^{2}}\,\cos \left( x+z \right)dx\,dy\,dz}\,\) con $C$ definito dalle seguenti espressioni matematiche: $0\le z\le \frac{\pi }{2}-x$ e $ 0 \le y \le \sqrt[3]{x}$

Soluzione

L’insieme \(C\) rappresenta tra due solidi normali rispettivamente al piano \(z=0\) e al piano \(y=0\). Ragionare sul solido generato è piuttosto complicato come d’altronde lo è provare a disegnarlo. E’ piuttosto agevole invece integrare per fili.

Facciamo alcune osservazioni: \(0\le z\le \frac{\pi }{2}-x\,\,\Rightarrow \,\,\,x\le \frac{\pi }{2}\). Inoltre \(0\le y\le \sqrt[3]{x}\,\,\Rightarrow \,\,\,x\ge 0\) e mettendo insieme queste due limitazioni si ha che \(0\le x\le \frac{\pi}{2}\).

 dove \(\theta \) è l’angolo misurato rispetto al semiasse positivo delle \(x\) e \(\phi \) è l’angolo misurato rispetto al semiasse positivo delle \(z\) e si ha che la matrice Jacobiana ha determinante\(\det \mathbf{J}={{\rho }^{2}}\sin \phi \).

Si ha in coordinate sferiche \({{x}^{2}}+{{y}^{2}}={{\rho }^{2}}{{\sin }^{2}}\phi \). Sostituendo si ha che .

Per quanto riguarda la sfera invece si \(\rho \le 1\) con \(\theta \le \left[ 0,\frac{\pi }{2} \right]\) . In coordinate sferiche è possibile integrare per raggi.

Da cui \(\int\limits_{C}{z\,dx\,dy\,dz}\,\,=\int\limits_{\rho =0}^{1}{\int\limits_{\phi =0}^{2\pi }{\int\limits_{\theta =0}^{\frac{\pi }{2}}{\rho \cos \theta \,{{\rho }^{2}}{{\sin }^{2}}\phi \,d\rho \,d\phi \,d\theta }}}+\int\limits_{\theta =\frac{\pi }{2}}^{\pi }{\int\limits_{\phi =0}^{2\pi }{\int\limits_{\rho =0}^{\,\,\frac{1}{\sin \phi +\cos \phi }}{\rho \cos \theta \,{{\rho }^{2}}{{\sin }^{2}}\phi \,d\rho \,d\phi \,d\theta }}}=\)

Esercizio 6 – Calcolo di integrale triplo

Calcolare \(\int\limits_{C}{\frac{1}{{{y}^{2}}+1}dxdydz}\,\) con $C$ dato dalle condizioni $1 \le y \le 2$ e $y \le {\left(\frac{x}{3}\right)}^{2}+{\left(\frac{z}{2}\right)}^{2}$

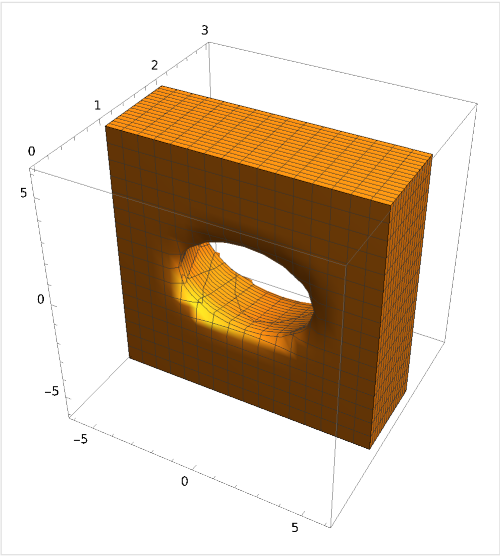
Soluzione 1

In coordinate ellittiche

\(x=3\rho \cos \theta ,\,\,\,z=2\rho \cos \theta ,\,\,\,\,y=y,\,\,\,\det \mathbf{J}=3\cdot 2\rho \)

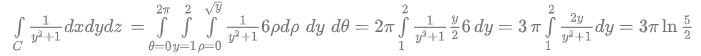
Soluzione 2

Stratificazione. Il volume elementare dello strato \(y\)è \(S(y)\,dy\) , dove \(S\left( y \right)\) è l’area della sezione \(y\) di equazione \[\frac{{{x}^{2}}}{{{\left( 3\sqrt{y} \right)}^{2}}}+\frac{{{z}^{2}}}{{{\left( 2\sqrt{y} \right)}^{2}}}=1\] e vale \(S\left( y \right)=2\sqrt{y}3\sqrt{y}\pi =6\pi y\)

Integrali Tripli

Lezioni di Analisi Matematica 2