14. Soluzione integrale triplo in coordinate cilindriche
$\iiint\limits_{A}{( 1+xy )dxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,{{z}^{2}}+1\le {{x}^{2}}+{{y}^{2}}\le z+3 \}$
L’insieme di integrazione è rappresentato in figura.
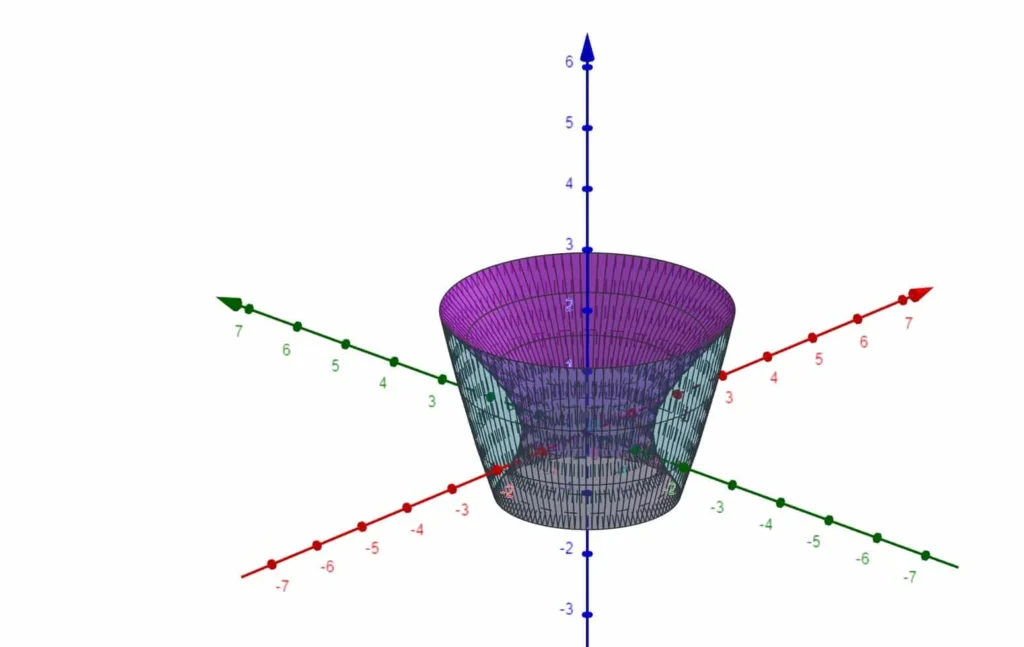
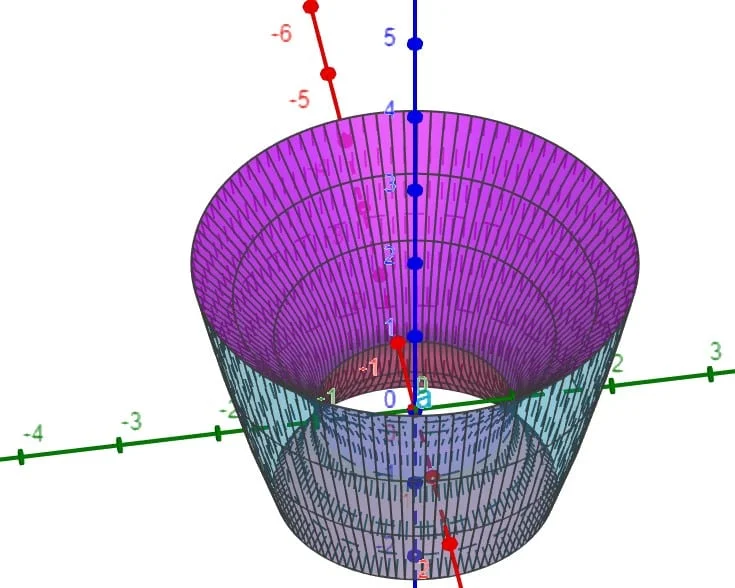
Usiamo il cambio di coordinate che ci permette di passare dalle coordinate cartesiane a quelle cilindriche.
Le equazioni che esprimono le coordinate cilindriche nello spazio sono:
$ \begin{cases} x = \rho \cos \theta \\ y = \rho \sin \theta \\ z = z \end{cases} $
Facciamo il cambio di coordinate nell’insieme di integrazione, facendo il cambio di variabili nelle disequazioni e risolvendole in forma algebrica.
${{z}^{2}}+1\le z+3$
${{z}^{2}}-z-2\le 0$
$-1\le z\le 2$
${{z}^{2}}+1\ge 0 \forall z$
${{z}^{2}}+1\le {{\rho }^{2}}\le z+3$
$\sqrt{{{z}^{2}}+1}\le \rho \le \sqrt{z+3}$
L’insieme A in coordinate polari diventa:
${A}’=\{ (\rho ,\theta ,z)\in {{\mathbb{R}}^{3}}:-1\le z\le 2,0\le \theta \le 2\pi ,\sqrt{{{z}^{2}}+1}\le \rho \le \sqrt{z+3}\, \}$
Facciamo il cambio di coordinate nell’integrale ricordando di moltiplicare la funzione integranda per il modulo del determinante della matrice Jacobiana.
$\iiint\limits_{A}{( 1+xy )dxdydz}=$ $\iiint\limits_{{{A}’}}{( 1+\rho \cos \theta \rho \sin \theta )\rho d\rho d\theta dz}=$ $\iiint\limits_{{{A}’}}{\rho +\frac{{{\rho }^{3}}}{2}\sin ( 2\theta )d\rho d\theta dz}=$
Aggiungiamo gli estremi di integrazione nell’integrale triplo:
$\int\limits_{\theta =0}^{2\pi }{\int\limits_{z=-1}^{2}{\int\limits_{\rho =\sqrt{{{z}^{2}}+1}}^{\sqrt{z+3}}{\rho +\frac{{{\rho }^{3}}}{2}\sin ( 2\theta )dz}d\rho }d\theta }=$
Spezziamo l’integrale nella somma di due integrali tripli
$\int\limits_{\theta =0}^{2\pi }{\int\limits_{z=-1}^{2}{\int\limits_{\rho =\sqrt{{{z}^{2}}+1}}^{\sqrt{z+3}}{\frac{{{\rho }^{3}}}{2}\sin ( 2\theta )dz}d\rho }d\theta }+\int\limits_{\theta =0}^{2\pi }{\int\limits_{z=-1}^{2}{\int\limits_{\rho =\sqrt{{{z}^{2}}+1}}^{\sqrt{z+3}}{\rho dz}d\rho }d\theta }=$
$\int\limits_{\theta =0}^{2\pi }{\sin ( 2\theta )d\theta }\cdot \int\limits_{z=-1}^{2}{\int\limits_{\rho =\sqrt{{{z}^{2}}+1}}^{\sqrt{z+3}}{\frac{{{\rho }^{3}}}{2}dz}d\rho }+\int\limits_{\theta =0}^{2\pi }{\int\limits_{z=-1}^{2}{\int\limits_{\rho =\sqrt{{{z}^{2}}+1}}^{\sqrt{z+3}}{\rho dz}d\rho }d\theta }=$
Il primo integrale fa zero $\int\limits_{\theta =0}^{2\pi }{\sin ( 2\theta )d\theta }\cdot \int\limits_{z=-1}^{2}{\int\limits_{\rho =\sqrt{{{z}^{2}}+1}}^{\sqrt{z+3}}{\frac{{{\rho }^{3}}}{2}dz}d\rho }=0$ perché $\int\limits_{\theta =0}^{2\pi }{\sin ( 2\theta )d\theta }=0$
Calcoliamo il risultato del secondo integrale:
$\int\limits_{\theta =0}^{2\pi }{d\theta \cdot \int\limits_{z=-1}^{2}{[ \frac{{{\rho }^{2}}}{2} ]_{\sqrt{{{z}^{2}}+1}}^{\sqrt{z+3}}d\rho }}=$ $2\pi \int\limits_{z=-1}^{2}{[ \frac{z+3-{{z}^{2}}-1}{2} ]d\rho }$=$\pi \int\limits_{z=-1}^{2}{z+2-{{z}^{2}}d\rho }=\frac{9}{2}\pi $
Il risultato dell’integrale triplo è pari a:
$\iiint\limits_{A}{( 1+xy )dxdydz}=\frac{9}{2}\pi $
Abbiamo concluso l’integrale triplo online. Continua a navigare sul sito per leggere altri esempi.
Approfondimento
Un esercizio molto utile è quello di provare a descrivere la superficie esterna dell’insieme di integrazione.
Riportiamo una possibile soluzione:
${{\Sigma }_{1}}=( \rho \cos \theta ,\rho \sin \theta ,{{\rho }^{2}}-3 )$ , $0\le \theta \le 2\pi $, $\sqrt{2}\le \rho \le \sqrt{5}$
${{\Sigma }_{2}}={{\Sigma }_{a}}\cup {{\Sigma }_{b}}$
${{\Sigma }_{a}}=( \rho \cos \theta ,\rho \sin \theta ,\sqrt{{{\rho }^{2}}-1} )$ , $0\le \theta \le 2\pi $, $1\le \rho \le \sqrt{5}$
${{\Sigma }_{b}}=( \rho \cos \theta ,\rho \sin \theta ,-\sqrt{{{\rho }^{2}}-1} )$, $0\le \theta \le 2\pi $, $1\le \rho \le \sqrt{2}$
