4. Integrale Triplo con valori assoluti – Cambio coordinate e Matrice Jacobiana
$\iiint\limits_{A}{zdxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,\,|x-z|+|y-z|\le 1+z,\,\,\,\,0\le z\le 1 \}$
Continua a leggere lo svolgimento integrale triplo. Come si può notare l’insieme di integrazione è espresso da espressioni che contengono valori assoluti. In questo caso, con un opportuno cambio di coordinate lineare, di cui è facile calcolarne la matrice Jacobiana e il determinante, è possibile semplificare l’insieme di integrazione e ottenere una figura geometrica nota, che altro non è che un quadrato.
Ti anticipo che il risultato dell’integrale è $\frac{17}{6}$, ma prima di continuare a leggere la soluzione è una buona idea provare a risolverlo da solo. È sempre una buona pratica provare a ragionare per cercare di arrivarci da soli al risultato. Sia se ci riuscirai sia se non ci riuscirai, avrai comunque sviluppato un tuo metodo di ragionamento matematico.
Per prima cosa facciamo un cambio di coordinate lineare in modo da rendere più semplice la descrizione dell’insieme.
$\begin{cases}x – z = r \\y – z = s \\z = z\end{cases}$
da cui si ottiene il seguente cambio di coordinate:
$\begin{cases}x = r + z \\y = s + z \\z = z\end{cases}$
La matrice Jacobiana per questo cambio di coordinate vale:
$J=\left[ \begin{matrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \\\end{matrix} \right]$
Il modulo del determinante della matrice Jacobiana vale uno $|\det J|=1$
L’insieme $A$ nel nuovo sistema di coordinate è dato da:
${A}’=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,\,|r|+|s|\le 1+z,\,\,\,\,0\le z\le 1 \}$
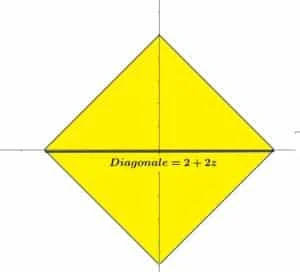
Osserviamo che la sezione del solido ${A}’$ con z fissato è un quadrato avente diagonale $D=2+2z$ come rappresentato in figura, rappresentato dalla disequazione $|r|+|s|\le 1+z$.
Poiché la sezione quadrata è ottenuta fissando z, si ha che la funzione integranda $f(x,y,z)=z$ è costante su tutta la superficie del quadrato. Possiamo pertanto scegliere come volume elementare il parallelepipedo avente come base il quadrato giallo rappresentato in figura e come altezza dz e si ha quindi $dV=S(z)dz$, dove $S(z)$ rappresenta la superficie del quadrato. Essa può essere calcolata a partire dalla diagonale attraverso la formula $S( z )=\frac{{{D}^{2}}}{2}=2{{(1+z)}^{2}}$ . L’integrale quindi diventa:
$\iiint\limits_{A}{zdxdydz}=$ $\iiint\limits_{A}{zdV}=$ $\int\limits_{0}^{1}{zS(z)dz}=$ $\int\limits_{0}^{1}{z\cdot 2{{(1+z)}^{2}}dz}=$ $\int\limits_{0}^{1}{2z(1+{{z}^{2}}+2z)dz}=$ $\int\limits_{0}^{1}{2z+2{{z}^{3}}+4{{z}^{2}}dz}=$ $[ {{z}^{2}}+\frac{1}{2}{{z}^{4}}+\frac{4}{3}{{z}^{3}} ]_{0}^{1}=\frac{17}{6}$
Possiamo concludere che il risultato dell’integrale triplo è $\frac{17}{6}$:
