Esercizi svolti sul teorema di Guldino

Il Teorema di Guldino è un principio fondamentale nella matematica e nell’ingegneria, particolarmente nell’ambito della geometria e della meccanica e in questa pagina andremo ad esplorare 3esercizi Teorema di Guldino . Questo teorema, chiamato anche le regole di Pappo-Guldino, fornisce un metodo elegante e potente per calcolare il volume di un solido di rotazione e l’area delle superfici generate dalla rotazione di una figura piana attorno a un asse. La bellezza di questo teorema risiede nella sua capacità di semplificare calcoli che altrimenti sarebbero complessi, utilizzando le proprietà geometriche delle figure coinvolte.

In questa pagina dedicata agli esercizi Teorema di Guldino, esploreremo una varietà di problemi che dimostrano l’applicazione pratica e teorica di questo principio. Attraverso esempi guidati, esercizi risolti, e problemi proposti, gli studenti saranno invitati a mettere in pratica le loro conoscenze, affinando la comprensione del teorema e sviluppando la capacità di applicarlo in contesti diversi. Saranno presentati esercizi che variano per difficoltà, da quelli più semplici e diretti a problemi che richiedono una riflessione più profonda e un’applicazione creativa del teorema.

Ogni esercizio sarà accompagnato da una spiegazione dettagliata dei passaggi risolutivi, fornendo non solo la soluzione ma anche il ragionamento sottostante. Ciò aiuterà gli studenti a costruire una solida comprensione concettuale del teorema, oltre a sviluppare competenze matematiche fondamentali. L’obiettivo è di rendere gli studenti non solo capaci di risolvere i problemi proposti, ma anche di applicare il Teorema di Guldino in nuovi contesti, stimolando così un’apprendimento profondo e duraturo.

Attraverso questa pagina, gli studenti scopriranno il potere e l’eleganza del Teorema di Guldino, arricchendo la loro cassetta degli attrezzi matematica e ingegneristica. Saranno incoraggiati a esplorare oltre i confini dei problemi classici, applicando la teoria a casi reali e a situazioni innovative. In questo modo, il capitolo non solo educa ma ispira, aprendo la porta a un mondo di possibilità matematiche e ingegneristiche.

Esercizio 1 svolto – esercizi Teorema di Guldino

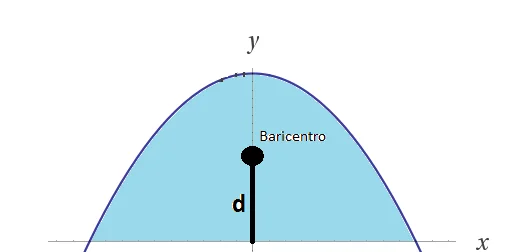
Calcolare il volume del solido ottenuto facendo ruotare \(S=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}:\,\,0\le y\le 1-{{x}^{2}} \right\}\) intorno all’asse \(x\).

Definizione del Problema

L’insieme $S$ è definito da:

$S = \{ (x, y) \in \mathbb{R}^2 : 0 \le y \le 1 – x^2 \}$

Questo descrive una parabola che si apre verso il basso, con vertice in $(0, 1)$ e intersezioni con l’asse $x$ in $(-1, 0)$ e $(1, 0)$.

Calcolo della Coordinata $d$ del Baricentro

La coordinata $d = y_B$ del baricentro rispetto all’asse $x$ si ottiene come il rapporto tra il momento statico dell’area $S$ rispetto all’asse $x$ e l’area di $S$ stessa:

$d = \frac{\int_S y \, dS}{A(S)}$

L’area di $S$ ($A(S)$) si può trovare come:

$A(S) = \int_{-1}^{1} (1 – x^2) \, dx$

Il momento statico si calcola come:

$\int_S y \, dS = \int_{-1}^{1} \int_{0}^{1-x^2} y \, dy \, dx$

Calcolo del Volume del Solido di Rotazione

Sostituendo $d$ nell’espressione del volume dato dal teorema di Guldino, abbiamo:

$V = 2\pi \int_{-1}^{1} \left( \int_{0}^{1-x^2} y \, dy \right) dx$

Svolgendo l’integrale interno rispetto a $y$, otteniamo il quadrato di $y$ diviso 2, valutato tra 0 e $1-x^2$, il che ci dà:

$V = 2\pi \int_{-1}^{1} \left[ \frac{(1-x^2)^2}{2} \right] dx$

Espandendo $(1-x^2)^2$ e semplificando, si ottiene:

$V = \pi \int_{-1}^{1} (1 – 2x^2 + x^4) dx$

Questo integrale è semplice da valutare, poiché si tratta di un polinomio. Integrando termine per termine, otteniamo:

$V = \pi \left[ x – \frac{2}{3}x^3 + \frac{1}{5}x^5 \right]_{-1}^{1}$

Calcolando il valore dell’integrale tra -1 e 1, si trova:

$V = \pi \left( \left(1 – \frac{2}{3} + \frac{1}{5}\right) – \left(-1 + \frac{2}{3} – \frac{1}{5}\right) \right)$

$V = \pi \left( \frac{4}{3} – \frac{2}{5} \right)$

$V = \pi \left( \frac{8}{15} \right)$

$V = \frac{8\pi}{15}$

Esercizio 2 svolto – esercizi Teorema di Guldino

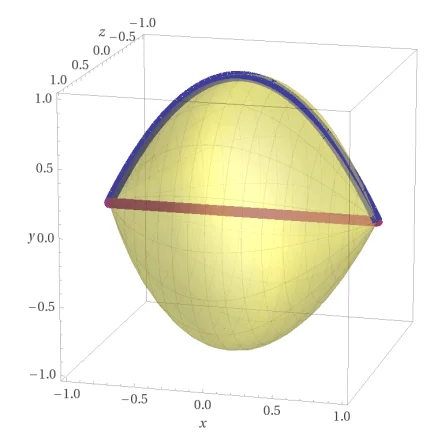
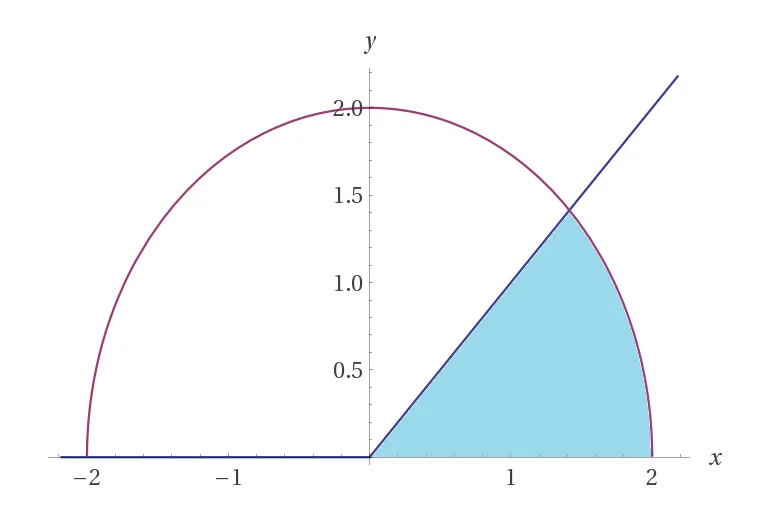
Calcolare il volume del solido ottenuto facendo ruotare \(S=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}:\,\,{{x}^{2}}+{{y}^{2}}\le 4,\,\,0\le y\le x \right\}\) intorno all’asse \(x\).

Definizione del Problema

Il problema riguarda il calcolo del volume di un solido generato dalla rotazione di un’area definita intorno all’asse $x$. L’area in questione, $S$, è delimitata da una circonferenza di raggio $2$ (cioè $x^2 + y^2 \le 4$) e dalla condizione $0 \le y \le x$. Ciò significa che consideriamo solo la parte dell’area che si trova sia nel primo quadrante che sotto la bisettrice del primo e terzo quadrante (la retta $y = x$).

Intersezione tra Retta e Circonferenza

Per trovare i limiti di integrazione per il calcolo del volume, dobbiamo determinare i punti di incontro tra la retta $y = x$ e la circonferenza $x^2 + y^2 = 4$. Sostituendo $y$ con $x$ nell’equazione della circonferenza, otteniamo $x = \sqrt{4 – x^2}$, che risolta dà come soluzione positiva $x = \sqrt{2}$. Questo punto di intersezione è cruciale per definire i limiti del nostro integrale.

Calcolo del Volume del Cono

La rotazione della regione definita dalla retta $y = x$ intorno all’asse $x$ genera un cono. La distanza dal centro della circonferenza al punto di intersezione ($\sqrt{2}$) serve sia come altezza $h$ che come raggio di base $r$ del cono. Utilizzando la formula del volume di un cono $\frac{1}{3}\pi r^2 h$, otteniamo un volume di $\frac{2\sqrt{2}}{3}\pi$.

Calcolo del Volume della Calotta Sferica

La parte della circonferenza che ruota intorno all’asse $x$ genera una calotta sferica. La sua altezza $h$ è la differenza tra il raggio della sfera e la distanza dall’asse $x$ al punto di intersezione, quindi $2 – \sqrt{2}$. Con $r = 2$ come raggio della sfera intera, il volume della calotta è dato da $\pi h^2 \left(r – \frac{h}{3}\right)$, risultando in $\frac{2}{3}\pi (8 – 5\sqrt{2})$.

Somma dei Volumi

Il volume totale del solido di rotazione è la somma dei volumi del cono e della calotta sferica, che porta a $V = \frac{8}{3}\pi (2 – \sqrt{2})$.

Conclusione

Questo metodo di calcolo illustra come la combinazione di principi geometrici semplici e l’uso di integrazioni possa portare alla soluzione di problemi apparentemente complessi di calcolo del volume. Ogni passaggio, dalla determinazione dei punti di intersezione alla somma dei volumi individuali, contribuisce a una comprensione più profonda della struttura del solido e del processo di calcolo.

Esercizio 3 svolto – esercizi Teorema di Guldino

Calcolare il volume del solido ottenuto facendo ruotare \(S=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}:\,\,{{x}^{2}}+{{y}^{2}}\le 2y,\,\,y\ge 1 \right\}\) intorno all’asse \(x\).

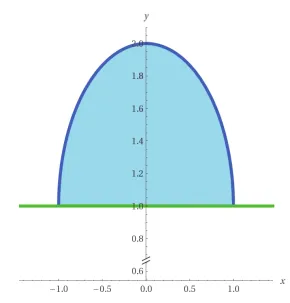
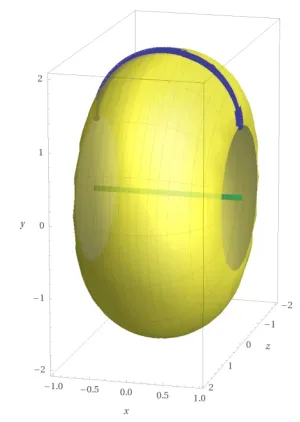
Per calcolare il volume del solido ottenuto dalla rotazione attorno all’asse $x$ della regione definita da $S=\{ (x,y) \in \mathbb{R}^2 : x^2 + y^2 \le 2y, y \ge 1 \}$, possiamo sfruttare il teorema di Guldino. La regione descritta da $S$ corrisponde a una semicirconferenza di raggio unitario centrata in $C=(0,1)$, tagliata da una retta orizzontale $y=1$.

Trasformazione in Coordinate Polari Traslate

Per facilitare il calcolo, passiamo a coordinate polari traslate centrando il sistema di riferimento in $C=(0,1)$, così da avere:

$(x, y) = (\rho \cos \theta, \rho \sin \theta + 1)$

dove $\rho$ è il raggio della circonferenza (che va da $0$ a $1$, dato che il raggio della semicirconferenza è unitario) e $\theta$ varia da $0$ a $\pi$ per coprire tutta la semicirconferenza superiore.

Calcolo del Volume Usando il Teorema di Guldino

Il teorema di Guldino afferma che il volume $V$ del solido generato dalla rotazione attorno all’asse $x$ di una regione piana è dato da:

$V = 2\pi \iint\limits_S y \, ds$

dove $y$ è la distanza dell’elemento di area $ds$ dall’asse di rotazione.

Sostituendo la trasformazione in coordinate polari traslate, otteniamo:

$V = 2\pi \int\limits_0^1 \int\limits_0^\pi (\rho \sin \theta + 1) \rho \, d\theta \, d\rho$

Svolgimento degli Integrali

Calcoliamo separatamente i due integrali:

1. L’integrale rispetto a $\theta$ è:

$\int\limits_0^\pi (\rho \sin \theta + 1) \, d\theta = \left[ -\rho \cos \theta + \theta \right]_0^\pi = 2\rho + \pi$

2. Sostituendo il risultato dell’integrale rispetto a $\theta$ nell’integrale rispetto a $\rho$, otteniamo:

$V = 2\pi \int\limits_0^1 (2\rho + \pi) \rho \, d\rho = 2\pi \left( \int\limits_0^1 2\rho^2 \, d\rho + \pi \int\limits_0^1 \rho \, d\rho \right)$

$V = 2\pi \left( \left[ \frac{2\rho^3}{3} \right]_0^1 + \pi \left[ \frac{\rho^2}{2} \right]_0^1 \right) = 2\pi \left( \frac{2}{3} + \frac{\pi}{2} \right) = \frac{4\pi}{3} + \pi^2$

Quindi, il volume del solido generato dalla rotazione della semicirconferenza intorno all’asse $x$ è $\frac{4}{3}\pi + \pi^2$ Questo calcolo mostra come l’uso delle coordinate polari, insieme al teorema di Guldino, semplifichi significativamente la determinazione del volume di solidi di rotazione complessi.

Lezioni di Analisi Matematica 2