Indice dei contenuti
- Cambio di coordinate negli integrali tripli
- Cambio di coordinate negli integrali tripli: le coordinate cilindriche
- Cambio di coordinate negli integrali tripli: Coordinate cilindriche ellittiche
- Cambio di coordinate negli integrali tripli: Coordinate sferiche
- Coordinate sferiche ellissoidali o coordinate sferiche ellittiche scalate
- Cambio di coordinate definite da un’applicazione lineare
Cambio di coordinate negli integrali tripli
In generale un cambio di coordinate negli integrali tripli si ottiene attraverso una funzione vettoriale:
$h:\mathbb{R}^3 \to \mathbb{R}^3$
(a volte chiamata mappa) e rappresentata da:
$ \begin{cases} x=h_1({x}’,{y}’,{z}’) \\ y=h_2({x}’,{y}’,{z}’) \\ z=h_3({x}’,{y}’,{z}’) \\ \end{cases} $
La matrice Jacobiana è data da:
$J=\left[\begin{matrix} \frac{\partial {{h}_{1}}}{\partial x} & \frac{\partial {{h}_{1}}}{\partial y} & \frac{\partial {{h}_{1}}}{\partial z} \\ \frac{\partial {{h}_{2}}}{\partial x} & \frac{\partial {{h}_{2}}}{\partial y} & \frac{\partial {{h}_{2}}}{\partial z} \\ \frac{\partial {{h}_{3}}}{\partial x} & \frac{\partial {{h}_{3}}}{\partial y} & \frac{\partial {{h}_{3}}}{\partial z} \\ \end{matrix}\right]$
Attraverso questa funzione è possibile passare dal sistema di coordinate $(x,y,z)$ ad un nuovo sistema di coordinate $({x}’,{y}’,{z}’)$.
Il mappaggio attraverso la funzione $h$ deve essere essere fatto sia sull’insieme $A$ che nel nuovo sistema di coordinate diventa ${A}’$, sia sulla funzione che diventa $f(x,y,z)=f(h_1({x}’,{y}’,{z}’),h_2({x}’,{y}’,{z}’),h_3({x}’,{y}’,{z}’))$ , sia sul volume elementare che nel passare da un sistema di riferimento all’altro subisce una deformazione e se ne tiene conto attraverso il modulo del determinante della matrice Jacobiana e si ha $dxdydz=|detJ|{dx}'{dy}'{dz}’$.
Quindi nel nuovo sistema di coordinate l’integrale triplo diventa:
$\iiint\limits_{A}{f\left( x,y,z \right)dxdydz}=\iiint\limits_{{A}’}{f(h_1({x}’,{y}’,{z}’),h_2({x}’,{y}’,{z}’),h_3({x}’,{y}’,{z}’))|detJ|{dx}'{dy}'{dz}’}$
I principali sistemi di coordinate che si utilizzano per integrali tripli sono le coordinate cilindriche e sferiche.
Cambio di coordinate negli integrali tripli: le coordinate cilindriche
Il passaggio da coordinate cartesiane $(x, y, z)$ a coordinate cilindriche $(\rho, \theta, z)$ è un esempio di cambio di coordinate che si utilizza comunemente in matematica e fisica, specialmente quando si studiano problemi con simmetria cilindrica. La funzione che descrive questo cambio di coordinate è:
$\begin{cases}x = \rho \cos \theta \\y = \rho \sin \theta \\z = z\end{cases}$
dove:
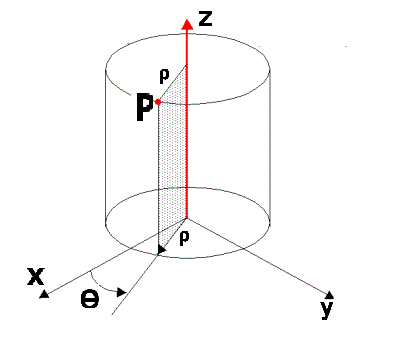
– $\rho$ è la distanza radiale del punto dall’asse $z$, ovvero la distanza della proiezione del punto sul piano $xy$ dall’origine.
– $\theta$ è l’angolo formato dalla proiezione del punto sul piano $xy$ rispetto all’asse $x$.
– $z$ rimane invariata rispetto al sistema di coordinate cartesiane.
Significato Geometrico di $\rho$ e $\theta$
– $\rho$ rappresenta la distanza del punto dalla linea verticale definita dall’asse $z$. Questo valore è sempre non negativo ($\rho \ge 0$).
– $\theta$ misura l’angolo in radianti tra l’asse positivo $x$ e la semiretta che parte dall’origine e passa per la proiezione del punto $P$ sul piano $xy$. L’angolo $\theta$ varia da $0$ a $2\pi$ radianti, coprendo un giro completo attorno all’asse $z$.
Calcolo del Determinante della Matrice Jacobiana
Il cambio di coordinate è accompagnato da una matrice Jacobiana, che aiuta a trasformare gli elementi di volume (o area) dal vecchio sistema di coordinate al nuovo. Per le coordinate cilindriche, la matrice Jacobiana ($J$) del cambio di coordinate è data da:
$J = \begin{bmatrix}\frac{\partial x}{\partial \rho} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z} \\\frac{\partial y}{\partial \rho} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z} \\\frac{\partial z}{\partial \rho} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z}\end{bmatrix}=\begin{bmatrix}\cos \theta & -\rho \sin \theta & 0 \\\sin \theta & \rho \cos \theta & 0 \\0 & 0 & 1\end{bmatrix}$
Il determinante $|detJ|$ di questa matrice Jacobiana è il fattore di scala che ci dice quanto cambia l’elemento di volume quando passiamo da coordinate cartesiane a cilindriche. Calcoliamo $|detJ|$:
$|detJ| = \begin{vmatrix}\cos \theta & -\rho \sin \theta & 0 \\\sin \theta & \rho \cos \theta & 0 \\0 & 0 & 1\end{vmatrix}= (1) \cdot \left( (\cos \theta)(\rho \cos \theta) – (-\rho \sin \theta)(\sin \theta) \right) = \rho$
Quindi, il determinante della matrice Jacobiana per il cambio di coordinate da cartesiane a cilindriche è $\rho$. Questo significa che, quando integriamo in coordinate cilindriche, dobbiamo moltiplicare l’integrand per $\rho$ per tener conto della trasformazione dell’area o del volume di integrazione.
Cambio di coordinate negli integrali tripli: Coordinate cilindriche ellittiche
Le coordinate che note come coordinate cilindriche ellittiche. In questo sistema di coordinate, ogni punto nello spazio è rappresentato da una tripla $(\rho, \theta, z)$, ma a differenza delle coordinate cilindriche standard, $\rho$ e $\theta$ sono usati per descrivere ellissi nel piano $xy$ anziché cerchi. Questo sistema è particolarmente utile per problemi con simmetria ellittica rispetto all’asse $z$.
Le trasformazioni sono definite come segue:
$\begin{cases}x = a \rho \cos \theta \\y = b \rho \sin \theta \\z = z\end{cases}$
dove:
– $a$ e $b$ sono costanti che determinano le dimensioni dell’ellisse nel piano $xy$.
– $\rho \geq 0$ è un fattore di scala che allontana il punto dall’origine lungo l’ellisse.
– $\theta \in [0, 2\pi)$ è l’angolo polare misurato nel piano dell’ellisse.
– $z$ è la coordinata lungo l’asse $z$, come nelle coordinate cilindriche standard.
Significato Geometrico
– $\rho$: Rappresenta il fattore di scala ellittico. Per un dato valore di $\rho$, tutti i punti giacciono su un’ellisse che è scalata proporzionalmente da quella definita da $\rho = 1$.
– $\theta$: Determina la posizione del punto sull’ellisse definita da $\rho$, proprio come l’angolo $\theta$ nelle coordinate polari standard determina la posizione su un cerchio.
– $z$: Mantiene il suo significato come la coordinata verticale, parallela all’asse $z$.
Calcolo del Determinante della Matrice Jacobiana
Per le coordinate cilindriche ellittiche, la matrice Jacobiana $J$ associata alla trasformazione è data da:
$J =\begin{bmatrix}\frac{\partial x}{\partial \rho} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z} \\\frac{\partial y}{\partial \rho} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z} \\\frac{\partial z}{\partial \rho} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z}\end{bmatrix}=\begin{bmatrix}a \cos \theta & -a \rho \sin \theta & 0 \\b \sin \theta & b \rho \cos \theta & 0 \\0 & 0 & 1\end{bmatrix}$
Il determinante di questa matrice Jacobiana è:
$|detJ| = (a \cos \theta)(b \rho \cos \theta)(1) – (-a \rho \sin \theta)(b \sin \theta)(0) + (0)(0)(0) – (0)(-a \rho \sin \theta)(1) = ab \rho \cos^2 \theta + ab \rho \sin^2 \theta = ab\rho$
Poiché $\cos^2 \theta + \sin^2 \theta = 1$, il determinante semplificato è $ab\rho$.
Il determinante $|detJ| = ab\rho$ indica il fattore di scala necessario per la conversione di elementi di volume (o area, per problemi bidimensionali) dal sistema di coordinate cilindriche ellittiche a quello cartesiano durante l’integrazione. Esso riflette l’influenza del fattore di scala ellittico $\rho$, insieme alle dimensioni ellittiche $a$ e $b$, sull’elemento di volume.
Cambio di coordinate negli integrali tripli: Coordinate sferiche
Il sistema di coordinate sferiche è uno dei sistemi di coordinate curvilinee più utilizzati per descrivere la posizione di un punto nello spazio tridimensionale, specialmente in contesti dove la simmetria sferica semplifica l’analisi matematica o fisica. Le coordinate sferiche sono definite da un raggio ($\rho$), un angolo azimutale ($\theta$), e un angolo polare ($\phi$).
Trasformazione in Coordinate Sferiche
Le relazioni che consentono di passare dalle coordinate cartesiane $(x, y, z)$ alle coordinate sferiche $(\rho, \theta, \phi)$ sono:
$\begin{cases}x = \rho \cos \theta \sin \phi \\y = \rho \sin \theta \sin \phi \\z = \rho \cos \phi\end{cases}$
dove:
– $\rho$ è la distanza del punto $P$ dall’origine degli assi ($O$), quindi $\rho \geq 0$.
– $\theta$ è l’angolo azimutale misurato nel piano $xy$ dall’asse positivo delle $x$, con $\theta \in [0, 2\pi]$.
– $\phi$ è l’angolo polare o colatitudine, misurato dall’asse positivo delle $z$ fino al punto $P$, con $\phi \in [0, \pi]$.
Significato Geometrico delle Variabili
– $\rho$ rappresenta la distanza radiale del punto dall’origine. È la distanza “diretta” dal punto $O$ al punto $P$ nello spazio.
– $\theta$ indica la direzione dell’ombra proiettata dal punto $P$ sul piano $xy$, cioè, l’angolo orizzontale rispetto all’asse delle $x$.
– $\phi$ rappresenta l’elevazione del punto $P$ rispetto al piano $xy$, ovvero, l’angolo verticale rispetto all’asse delle $z$.
Matrice Jacobiana e il suo Determinante
Per il cambio di coordinate da sferiche a cartesiane, la matrice Jacobiana ($J$) è definita come:
$J =\begin{bmatrix}\frac{\partial x}{\partial \rho} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial \phi} \\\frac{\partial y}{\partial \rho} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial \phi} \\\frac{\partial z}{\partial \rho} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial \phi}\end{bmatrix}=\begin{bmatrix}\cos \theta \sin \phi & -\rho \sin \theta \sin \phi & \rho \cos \theta \cos \phi \\\sin \theta \sin \phi & \rho \cos \theta \sin \phi & \rho \sin \theta \cos \phi \\\cos \phi & 0 & -\rho \sin \phi\end{bmatrix}$
Il determinante di questa matrice è:
$|detJ| = \rho^2 \sin \phi$
Questo risultato riflette il fattore di scala necessario quando si trasformano elementi di volume dal sistema di coordinate sferiche al sistema di coordinate cartesiane durante l’integrazione. Il termine $\rho^2 \sin \phi$ indica che il fattore di scala non è costante, ma varia in base alla posizione del punto nello spazio, conferendo una maggiore ponderazione alle regioni più lontane dall’origine e con maggior elevazione rispetto al piano $xy$.
Coordinate sferiche ellissoidali o coordinate sferiche ellittiche scalate
Le coordinate sferiche ellissoidali o coordinate sferiche ellittiche scalate sono una generalizzazione delle coordinate sferiche tradizionali, utilizzate per descrivere punti nello spazio tridimensionale che sono allungati o compressi lungo uno o più degli assi cartesiani. Questo sistema di coordinate è particolarmente utile per analizzare problemi geometrici o fisici che coinvolgono ellissoidi.
Definizione delle Coordinate
Il passaggio dalle coordinate cartesiane $(x, y, z)$ alle coordinate sferiche ellittiche scalate $(\rho, \theta, \phi)$ è dato dalle seguenti trasformazioni:
$\begin{cases}x = a \rho \cos \theta \sin \phi \\y = b \rho \sin \theta \sin \phi \\z = c \rho \cos \phi\end{cases}$
dove:
– $a$, $b$, e $c$ sono costanti positive che determinano il grado di allungamento o compressione dell’ellissoide lungo gli assi $x$, $y$, e $z$, rispettivamente.
– $\rho$ è la distanza radiale dal centro, che si estende fino al punto $P$ nello spazio.
– $\theta \in [0, 2\pi)$ è l’angolo azimutale, misurato nel piano $xy$ dall’asse positivo $x$.
– $\phi \in [0, \pi]$ è l’angolo polare, misurato dall’asse positivo $z$ al punto $P$.
Significato Geometrico
– $\rho$: rappresenta la “distanza” radiale scalata dall’origine al punto nello spazio, modificata dai fattori $a$, $b$, e $c$.
– $\theta$: determina la posizione del punto nell’ellisse proiettata sul piano $xy$, simile al ruolo di $\theta$ nelle coordinate polari o sferiche standard.
– $\phi$: misura l’elevazione del punto rispetto al piano $xy$, con un comportamento simile a quello delle coordinate sferiche standard.
Matrice Jacobiana e Determinante
Per calcolare il volume o l’area usando queste coordinate, è necessario determinare il fattore di scala fornito dal determinante della matrice Jacobiana delle trasformazioni. La matrice Jacobiana $J$ per queste trasformazioni è:
$J =\begin{bmatrix}a \cos \theta \sin \phi & -a \rho \sin \theta \sin \phi & a \rho \cos \theta \cos \phi \\b \sin \theta \sin \phi & b \rho \cos \theta \sin \phi & b \rho \sin \theta \cos \phi \\c \cos \phi & 0 & -c \rho \sin \phi\end{bmatrix}$
Il determinante $|detJ|$ di questa matrice Jacobiana è:
$|detJ| = abc \rho^2 \sin \phi$
Interpretazione del Determinante
Il determinante $|detJ| = abc \rho^2 \sin \phi$ rappresenta il fattore di scala necessario per la conversione di elementi di volume dal sistema di coordinate sferiche ellittiche scalate a quello cartesiano durante l’integrazione. Questo fattore tiene conto dell’allungamento o della compressione lungo ciascun asse, della distanza radiale $\rho$, e dell’angolazione $\phi$, fornendo una misura diretta di come il volume elementare nello spazio si espanda o si contragga a causa della trasformazione delle coordinate.
La presenza di $\sin \phi$ indica che il fattore di scala varia con l’angolo polare, aumentando per valori intermedi di $\phi$ e diminuendo vicino ai poli, mentre il termine $\rho^2$ riflette la crescita quadratica del volume con l’aumentare della distanza dall’origine, tipica dei sistemi sferici. Le costanti $a$, $b$, e $c$ modulano ulteriormente questa variazione in base alla forma ellittica specifica dello spazio considerato.
Cambio di coordinate definite da un’applicazione lineare
La trasformazione rappresenta da un’applicazione lineare generica dallo spazio $(u, v, w)$ allo spazio $(x, y, z)$, utilizzando una matrice di coefficienti $A$. Questa trasformazione è descritta dal sistema:
$\begin{cases}x = a_{1,1}u + a_{1,2}v + a_{1,3}w \\y = a_{2,1}u + a_{2,2}v + a_{2,3}w \\z = a_{3,1}u + a_{3,2}v + a_{3,3}w \end{cases}$
dove $a_{i,j}$ sono i coefficienti della matrice di trasformazione $A$.
Matrice di Trasformazione e Jacobiana
La matrice di trasformazione $A$ e la matrice Jacobiana $J$ della trasformazione sono identiche in questo contesto, e sono date da:
$A = J =\begin{bmatrix}a_{1,1} & a_{1,2} & a_{1,3} \\a_{2,1} & a_{2,2} & a_{2,3} \\a_{3,1} & a_{3,2} & a_{3,3}\end{bmatrix}$
Questa matrice rappresenta come ogni componente di $(x, y, z)$ dipende linearmente da $(u, v, w)$.
Biunivocità e Rango Massimo
Perché la trasformazione sia biunivoca (invertibile), ovvero perché esista una trasformazione inversa che mappi $(x, y, z)$ di nuovo in $(u, v, w)$ in modo unico, la matrice $A$ deve avere rango massimo. Nel contesto di una matrice $3 \times 3$, questo significa che $A$ deve essere di rango 3, il che si verifica se e solo se il determinante di $A$ è non nullo.
Calcolo del Determinante
Il determinante di $A$ (o $J$) è calcolato come:
$|detJ| = \begin{vmatrix}a_{1,1} & a_{1,2} & a_{1,3} \\a_{2,1} & a_{2,2} & a_{2,3} \\a_{3,1} & a_{3,2} & a_{3,3}\end{vmatrix}$
Questo determinante è dato dalla formula:
$|detJ| = a_{1,1}(a_{2,2}a_{3,3} – a_{2,3}a_{3,2}) – a_{1,2}(a_{2,1}a_{3,3} – a_{2,3}a_{3,1}) + a_{1,3}(a_{2,1}a_{3,2} – a_{2,2}a_{3,1})$
Implicazioni del Determinante Non Nullo
- Se $|detJ| \neq 0$, la trasformazione è biunivoca, e quindi esiste un’unica mappatura inversa da $(x, y, z)$ a $(u, v, w)$. Questo garantisce che la trasformazione sia invertibile e che ogni punto nello spazio di arrivo corrisponda a un unico punto nello spazio di partenza.
- Il valore di $|detJ|$ influisce sulle operazioni di integrazione, indicando il fattore di scala per il cambio di variabili in integrali multipli. Un determinante non nullo implica che la trasformazione preserva l’orientazione dello spazio, a patto che $|detJ|$ sia positivo. Se $|detJ|$ è negativo, l’orientazione viene invertita.
In sintesi, la trasformazione lineare definita ha proprietà molto potenti e utili in molti campi della matematica e della fisica, in particolare quando si tratta di cambiare le variabili in integrali o di risolvere sistemi di equazioni lineari.
