Indice dei contenuti
- PROBLEMA 1 – Simulazione 2 Aprile 2019
- PROBLEMA 2 – Simulazione 2 Aprile 2019
- QUESTIONARIO
- Soluzione Problema 1 – Simulazione 2 Aprile 2019
- Soluzione Problema 2 – Simulazione 2 Aprile 2019
- Soluzione Quesito 1 – Simulazione Seconda prova Maturità scientifica 2 Aprile 2019
- Soluzione Quesito 2 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
- Soluzione Quesito 3 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
- Soluzione Quesito 4 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
- Soluzione Quesito 5 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
- Soluzione Quesito 6 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
- Soluzione Quesito 7 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
si riporta il testo e la soluzione della simulazione della maturità scientifica, del 2 aprile 2019.
PROBLEMA 1 – Simulazione 2 Aprile 2019
Due fili rettilinei paralleli vincolati a rimanere nella loro posizione, distanti 1 m l’uno dall’altro e di lunghezza indefinita, sono percorsi da correnti costanti di pari intensità ma verso opposto; si indichi con i l’intensità di corrente, espressa in ampere (A). Si consideri un piano perpendicolare ai due fili sul quale è fissato un sistema di riferimento ortogonale Oxy, dove le lunghezze sono espresse in metri (m), in modo che i due fili passino uno per l’origine O e l’altro per il punto 𝐷(1,0), come mostrato in figura.
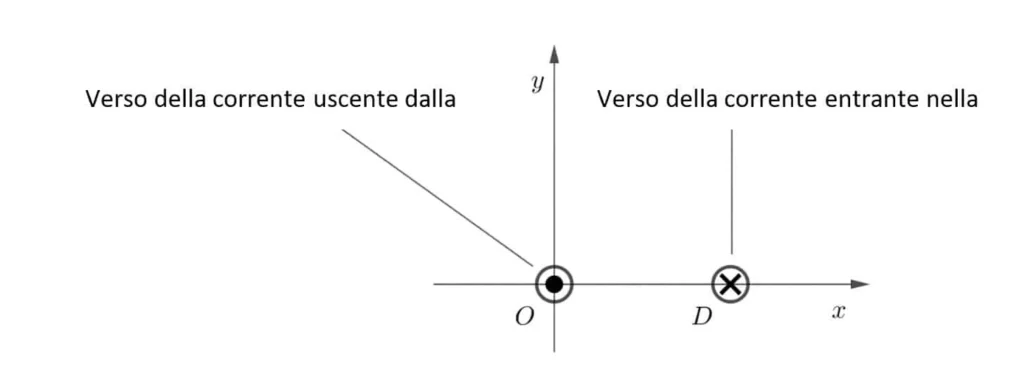
1. Verificare che l’intensità del campo magnetico 𝐵⃗ , espresso in tesla (T), in un punto 𝑃(𝑥,0) con 0<𝑥<1, è data dalla funzione \(𝐵(𝑥)=𝐾(\frac{1}{𝑥}+\frac{1}{1−𝑥})\), dove 𝐾 è una costante positiva della quale si richiede l’unità di misura. Stabilire quali sono la direzione e il verso del vettore al variare di 𝑥 nell’intervallo (0,1). Per quale valore di 𝑥 l’intensità di \(\vec{𝐵}\) è minima
2. Nella zona di spazio sede del campo \(\vec{𝐵}\) , una carica puntiforme q transita, ad un certo istante, per il punto 𝐶 (1/2, 0), con velocità di modulo \(𝑣_0\) nella direzione della retta di equazione 𝑥 =1/2. Descriverne il moto in presenza del solo campo magnetico generato dalle due correnti, giustificando le conclusioni
3. Indipendentemente da ogni riferimento alla fisica, studiare la funzione \(f(𝑥)=𝐾(\frac{1}{𝑥}+\frac{1}{1−𝑥})\) dimostrando, in particolare, che il grafico di tale funzione non possiede punti di flesso. Scrivere l’equazione della retta tangente al grafico di nel suo punto di ascissa 1/3 e determinare le coordinate dell’ulteriore punto d’intersezione tra \(r\) e il grafico di \(f\).
4. Calcolare il valore dell’integrale\[\int_{1/4}^{3/4}{f\left( x \right)\ dx}\]
Clicca per leggere la soluzione
PROBLEMA 2 – Simulazione 2 Aprile 2019
Assegnato un numero reale positivo , considerare le funzioni e così definite:
\(f(x)=\sqrt{x}(k-x)\) \(g(x)=x^2(x-k)\)
1. Provare che, qualunque sia k>0, nell’intervallo [0,k] il grafico di \(f\) ha un unico punto di massimo \(F(x_F,y_F)\) ed il grafico di \(g\) ha un unico punto di minimo \(G(x_G,y_G)\). Verificare che si ha \(x_G=2 x_F\) e \(y_G=-(y_G)^2\).
2. Verificare che, qualunque sia k>0, i grafici delle due funzioni sono ortogonali nell’origine, vale a dire che le rispettive rette tangenti in tale punto sono tra loro ortogonali. Determinare per quale valore positivo di \(k\) i due grafici si intersecano ortogonalmente anche nel loro ulteriore punto comune
D’ora in avanti, assumere k=1. In un riferimento cartesiano, dove le lunghezze sono espresse in metri (m), l’unione degli archi di curva di equazioni y=f(x) e y=g(x), per \(x\in[0,1]\) , rappresenta il profilo di una spira metallica. Sia \(S\) la regione piana delimitata da tale spira.
3. Supponendo che nella regione \(S\) sia presente un campo magnetico uniforme, perpendicolare al piano di \(S\) , avente intensità \(B_0=2,0\cdot 10^{-2}T\) , verificare che il valore assoluto del flusso di tale campo attraverso \(S\) è pari a \(B_0=7,0\cdot 10^{-3}T\)
4. Supporre che la spira abbia resistenza elettrica pari a \(R=70\Omega\) e che il campo magnetico, rimanendo perpendicolare al piano di \(S\), a partire dall’istante \(t_0=0s\), inizi a variare secondo la legge:\(B(t)=B_0 e^{-\omega t} cos(\omega t)\), con \(\omega=\pi rad/s\)e \(t\geqslant 0\) espresso in secondi (s). Esprimere l’intensità della corrente indotta nella spira in funzione di t, specificando in quale istante per la prima volta la corrente cambia verso.
Qual è il valore massimo di tale corrente per \(t\geqslant 0\)? Spiegare quale relazione esiste tra la variazione del campo che induce la corrente e il verso della corrente indotta.
Clicca per leggere la soluzione
QUESTIONARIO
QUESITO 1 – Simulazione 2 Aprile 2019
Assegnato \(k\in \mathbb{R}\) , si consideri la funzione g(x) così definita \(g(x)=\frac{(k-1)x^3+k x^2 – 3}{x-1}\):
Come va scelto il valore di \(k\) affinché il grafico di non abbia asintoti?
Come va scelto il valore di \(k\) affinché il grafico di abbia un asintoto obliquo?
Giustificare le risposte e rappresentare, nei due casi, i grafici delle funzioni ottenute.
Soluzione del quesito 1 della simulazione di maturità scientifica 2 aprile 2019
QUESITO 2 – Simulazione 2 Aprile 2019
Sia \(f\) una funzione pari e derivabile in \(\mathbb{R}\), sia \(g\) una funzione dispari e derivabile in \(\mathbb{R}\). Dimostrare che la funzione \(f\) è dispari e che la funzione \(g\) è pari. Fornire un esempio per la funzione \(f\) ed un esempio per la funzione \(g\) , verificando quanto sopra.
Soluzione del quesito 2 della simulazione di maturità scientifica 2 aprile 2019
QUESITO 3 – Simulazione 2 Aprile 2019
Si consideri la funzione \(f:(0,+\inf) \rightarrow \mathbb{R}\) così definita:
\[f\left( 1 \right)=\int_{1}^{x}{\ \frac{\cos \left( \frac{\pi }{3}t \right)}{t}}\ dt=0\]
Determinare l’equazione della retta tangente al grafico di \(f\) nel suo punto di ascissa \(1\).
Soluzione del quesito 3 della simulazione di maturità scientifica 2 aprile 2019
QUESITO 4 – Simulazione 2 Aprile 2019
Nello spazio tridimensionale, sia la retta passante per i punti \(A(-2,0,1)\) e \(B(0,2,1)\). Determinare le coordinate di un punto appartenente alla retta che sia equidistante rispetto ai punti \(C(5,1,-2)\) e \(D(1,3,4)\).
Soluzione del quesito 4 della simulazione di maturità scientifica 2 aprile 2019
QUESITO 5 – Simulazione 2 Aprile 2019
Emma fa questo gioco: lancia un dado con facce numerate da 1 a 6; se esce il numero 3 guadagna 3 punti, altrimenti perde 1 punto. Il punteggio iniziale è 0.
Qual è la probabilità che, dopo 4 lanci, il suo punteggio sia ancora 0?
Qual è la probabilità che, in una sequenza di 6 lanci, il punteggio non scenda mai sotto lo 0
Soluzione del quesito 5 della simulazione di maturità scientifica 2 aprile 2019
QUESITO 6 – Simulazione 2 Aprile 2019
Ai vertici di un quadrato \(ABCD\), di lato 2m, sono fissate quattro cariche elettriche. La carica in A è pari a 9 nC, la carica in B è pari a 2 nC, la carica in C è pari a 4 nC, la carica in D è pari a -3 nC. Supponendo che le cariche si trovino nel vuoto, determinare intensità, direzione e verso del campo elettrostatico generato dalle quattro cariche nel centro del quadrato.
Soluzione del quesito 6 della simulazione di maturità scientifica 2 aprile 2019
QUESITO 7 – Simulazione 2 Aprile 2019
Un protone, inizialmente in quiete, viene accelerato da una d.d.p. di 400 V ed entra, successivamente, in una regione che è sede di un campo magnetico uniforme e perpendicolare alla sua velocità.
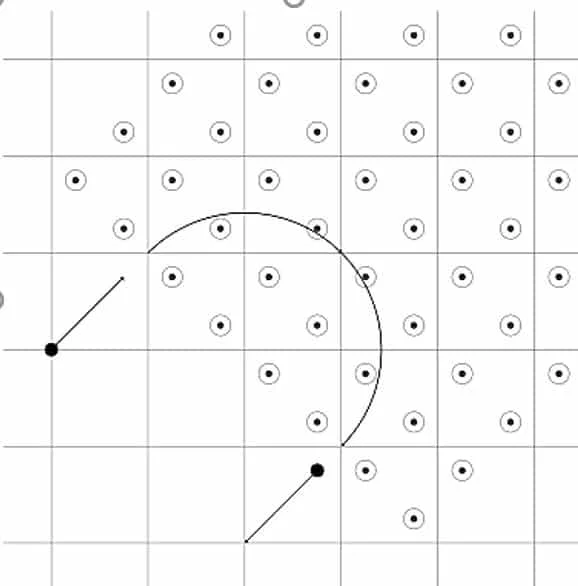
La figura illustra un tratto semicircolare della traiettoria descritta dal protone (i quadretti hanno lato 1,00 m). Determinare l’intensità di \(\vec{B}\)
Soluzione del quesito 7 della simulazione di maturità scientifica 2 aprile 2019
Soluzione Problema 1 – Simulazione 2 Aprile 2019
Soluzione prima domanda
Il verso del campo magnetico si ottiene applicando la regola della mano destra.
Mentre l’intensità si ottiene applicando la sovrapposizione degli effetti.
Il campo di induzione magnetica generato dal filo passante per l’origine è quello di un filo indefinito avente espressione:

\({{B}_{1}}\left( x \right)=\frac{{{\mu }_{0}}i}{2\pi x}\)
Il campo di induzione magnetica generato dal filo centrato in D(1,0) , ha la stessa espressione ma traslato di 1 rispetto all’asse x
\({{B}_{2}}\left( x \right)={{B}_{1}}\left( 1-x \right)=\frac{{{\mu }_{0}}i}{2\pi \left( 1-x \right)}\)
Il campo magnetico totale può essere calcolato applicando la sovrapposizione degli effetti. I due campi hanno lo stesso verso (regola della mano destra) pertanto è possibile sommare i rispettivi moduli.
\(B(x)={{B}_{1}}\left( x \right)+{{B}_{2}}\left( x \right)\)
\(B(x)=\frac{{{\mu }_{0}}i}{2\pi x}+\frac{{{\mu }_{0}}i}{2\pi \left( 1-x \right)}=\frac{\mu {}_{0}i}{2\pi }\left( \frac{1}{x}+\frac{1}{1-x} \right)\)
Posto \(K=\frac{\mu {}_{0}i}{2\pi }\) , si ha che la sua unità di misura è \(\left[ K \right]=T\cdot m\)
Soluzione seconda domanda
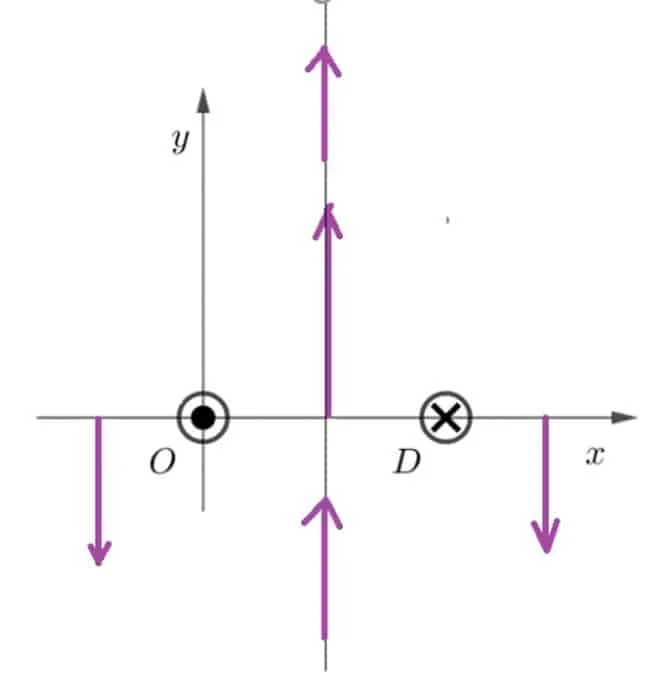
Le linee di campo magnetico lungo la retta x=1/2 sono parallele all’asse y, perché i punti su questa retta sono equidistanti da 0 e D e le correnti sono uguali. Lungo l’asse x=1/2 pertanto si annullano le componenti x, essendo queste ultime uguali e contrarie, mentre si sommano le componenti y.
Se una carica q viaggia a velocità \({{v}_{0}}\) lungo la retta x=1/2, non subisce alcuna forza per effetto del campo magnetico essendo quest’ultimo parallelo al vettore velocità. La forza di Lorentz \(\vec{F}=q{{\vec{v}}_{0}}\times \vec{B}=0\).
La carica viaggia di moto rettilineo uniforme lungo la retta x=1/2.
A destra del punto D lungo l’asse x, i moduli si sottraggono, ma prevale l’effetto del filo in D, essendo quest’ultimo più vicino.
A sinistra del punto O lungo l’asse x, i moduli si sottraggono, ma prevale l’effetto del filo in O, essendo quest’ultimo più vicino.
Questo è sufficiente per affermare che i campi non si annullano mai (hanno la stessa intensità solo al centro tra i due fili in x=1/2 dove però hanno lo stesso verso). In ogni caso è possibile arrivare alle stesse conclusioni attraverso l’equazione:
\(B(x)=K\left( \frac{1}{x}+\frac{1}{1-x} \right)=\frac{K}{x\left( 1-x \right)}\ne 0\)
\(\forall x\in \mathbb{R}-\left\{ 0,\,1 \right\}\)
Inoltre \(B(x)<0\) se \(x<0\,\vee x>1\) , il che giustifica i versi riportati in figura.
Soluzione terza domanda
Dominio di f(x): \(D=\mathbb{R}-\left\{ 0,\,1 \right\}\)
K è una costante positiva, quindi K>0.
Studio del segno: \(f(x)>0\) se \(0<x<1\)
La funzione è positiva tra 0 e 1 e negativa altrove. Non incontra mai l’asse x.
$$\underset{x\to \pm \infty }{\lim }\,K\left( \frac{1}{x}+\frac{1}{1-x}\ \right)=0$$
Pertanto $y=0$ è un asintoto orizzontale bilaterale.
$$\underset{x\to {0}^{+}}{\lim }\,K\left( \frac{1}{x}+\frac{1}{1-x}\ \right)=+\infty $$
$$\underset{x\to {1}^{-}}{\lim }\,K\left( \frac{1}{x}+\frac{1}{1-x}\ \right)=+\infty $$
$$\underset{x\to {0}^{-}}{\lim }\,K\left( \frac{1}{x}+\frac{1}{1-x}\ \right)=-\infty $$
$$\underset{x\to {1}^{+}}{\lim }\,K\left( \frac{1}{x}+\frac{1}{1-x}\ \right)=-\infty $$
Le rette x=0 e x=1 sono asintoti verticali.
Studio del segno della derivata prima:
\(f\left( x \right)=\frac{k}{x-{{x}^{2}}}\)\(\Rightarrow \) \({f}’\left( x \right)=-K\frac{1-2x}{{{\left( x-{{x}^{2}} \right)}^{2}}}\)
Si ha che \({f}’\left( x \right)>0\)\(\Rightarrow \)\(x<\frac{1}{2}\) da cui si deduce che in x=1/2 c’è un punto di massimo relativo. Passiamo a questo punto allo studio del segno della derivata seconda della funzione:
\({f}”\left( x \right)=2K\frac{-3{{x}^{2}}+3x-1}{{{\left( x-1 \right)}^{3}}{{x}^{3}}}>0\)
Il numeratore ha \(\Delta <0\) pertanto è sempre negativo sul dominio.
La derivata seconda è positiva per 0<x<1 e negativa altrove.
Poiché i cambi di concavità avvengono in corrispondenza di punti in cui la funzione non è definita, possiamo concludere che la funzione non ha flessi.
La retta tangente al punto di ascissa \(x=\frac{1}{3}\) ha equazione \(y={f}’\left( \frac{1}{3} \right)\left( x-\frac{1}{3} \right)+f\left( \frac{1}{3} \right)\)
\({f}’\left( \frac{1}{3} \right)=-\frac{27}{4}K\), \(f\left( \frac{1}{3} \right)=\frac{9}{2}K\)
Per cui l’equazione diventa: \(y=-\frac{27}{4}K\left( x-\frac{1}{3} \right)+\frac{9}{2}K\)

Soluzione quarta domanda
\(\int_{1/4}^{3/4}{f\left( x \right)\ dx}=K\int\limits_{1/4}^{3/4}{\left( \frac{1}{x}+\frac{1}{1-x}\ \right)dx}\)
\(\int_{1/4}^{3/4}{f\left( x \right)\ dx}=K\left[ \ln \left| x \right|-\ln \left| 1-x \right| \right]_{1/4}^{3/4}\)
\(\int_{1/4}^{3/4}{f\left( x \right)\ dx}=K\left[ \ln \left| \frac{x}{1-x} \right| \right]_{1/4}^{3/4}\)
\(\int_{1/4}^{3/4}{f\left( x \right)\ dx}=K\left[ \ln 3-\ln \frac{1}{3} \right]=2K\ln 3\)
Soluzione Problema 2 – Simulazione 2 Aprile 2019
Soluzione prima domanda
Dominio di f(x): \(x\ge 0\)
Studio il segno della derivata prima della funzione:
\({f}’\left( x \right)=\frac{k-3x}{2\sqrt{x}}>0\) \(\Rightarrow \)\(x<\frac{k}{3}\)
La funzione è crescente per \(x<\frac{k}{3}\) , è decrescente altrove sul dominio e presenta un punto di massimo relativo in corrispondenza di \({{x}_{F}}=\frac{k}{3}\) , \({{y}_{F}}=f\left( \frac{k}{3} \right)=2\frac{k\sqrt{k}}{3\sqrt{3}}\)
Dominio di g(x): Tutto l’asse dei reali.
Studio il segno della derivata prima della funzione:
\({g}’\left( x \right)=x\left( 3x-2k \right)>0\) \(\Rightarrow \) \(x<0\vee x>\frac{2k}{3}\)
La funzione è crescente per \(x<0\vee x>\frac{2k}{3}\), è decrescente altrove e presenta un punto di minimo relativo in corrispondenza di \({{x}_{G}}=\frac{2k}{3}=2{{x}_{F}}\) , \({{y}_{G}}=g\left( \frac{2k}{3} \right)=-\frac{4}{27}{{k}^{3}}=-y_{F}^{2}\)
Soluzione seconda domanda
Per quanto riguarda la prima richiesta, bisogna verificare che le due rette tangenti nell’origine degli assi (osserviamo che entrambi le funzioni passano per l’origine).
Si ha che f(x) non è derivabile nell’origine e che
\(\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,{f}’\left( x \right)=\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{k-3x}{2\sqrt{x}}=+\infty \) \(\Rightarrow\) la retta tangente al grafico di f(x) nell’origine è l’asse y.
\(\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,{g}’\left( x \right)=\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,x\left( 3x-2k \right)=0\) \(\Rightarrow \) la retta tangente al grafico di g(x) nell’origine è l’asse x.
I grafici sono ortogonali, perché le rispettive rette tangenti sono gli assi cartesiani.
Per quanto concerne la seconda richiesta, si ha invece che le due funzioni si incontrano ulteriormente nel punto che si ricava risolvendo l’equazione f(x)=g(x)
\(\sqrt{x}\ (k-x)={{x}^{2}}\left( x-k \right)\)\(\Rightarrow \) L’ulteriore punto in comune si trova nel punto di ascissa x=k e ordinata y=0.
I grafici sono ortogonali, se i coefficienti angolari delle rette tangenti, ovvero la derivata prima calcolata in x=k, sono antireciproci.
\({{m}_{1}}={f}’\left( k \right)=-\sqrt{k}\)
\({{m}_{2}}={g}’\left( k \right)={{k}^{2}}\)
\({{m}_{1}}=-\frac{1}{{{m}_{2}}}\) \(\Rightarrow \) \({{k}^{2}}=\frac{1}{\sqrt{k}}\) \(\Rightarrow\) \(k=1\)
Soluzione terza domanda
Per il calcolo del flusso attraverso la superficie S, procediamo attraverso la definizione di flusso:
\({{\Phi }_{S}}\left( {\vec{B}} \right)=\int_{S}{\vec{B}\cdot \hat{n}\,dS}\)
La normale alla superficie è l’asse z, che forma un angolo nullo con il vettore (\vec{B}), si può pertanto semplificare l’integrale come segue:
\({{\Phi }_{S}}\left( {\vec{B}} \right)=\) \({{B}_{0}}\int_{S}{dS}={{B}_{0}}\int\limits_{0}^{1}{f(x)-g(x)\,dx}=\) \({{B}_{0}}\int\limits_{0}^{1}{\left( 1-x \right)\sqrt{x}+(1-x){{x}^{2}}\,dx}=\)
\({{B}_{0}}\int\limits_{0}^{1}{{{x}^{1/2}}-{{x}^{3/2}}+{{x}^{2}}-{{x}^{3}}\,dx}=\) \({{B}_{0}}\left[ \frac{2}{3}{{x}^{3/2}}-\frac{2}{5}{{x}^{5/2}}+\frac{{{x}^{3}}}{3}-\frac{{{x}^{4}}}{4} \right]_{0}^{1}=\) \(\frac{7}{20}\,{{B}_{0}}=7,0\cdot {{10}^{-3}}\ Wb\)
Soluzione quarta domanda
Sfruttando i calcoli del punto precedente possiamo scrivere l’espressione del flusso magnetico\({{\Phi }_{S}}\left( {\vec{B}} \right)=\frac{7}{20}\,B(t)\) .
A partire da quest’ultima è possibile ricavare l’espressione della forza elettromotrice indotta nella spira attraverso la legge di Faraday-Newman:
\(fem=-\frac{\partial {{\Phi }_{S}}\left( {\vec{B}} \right)}{\partial t}=-\frac{7}{20}\,{B}'(t)=\) \(\frac{7}{20}\,{{B}_{0}}\ \omega {{e}^{-\omega t}}\left[ \cos \left( \omega t \right)+\sin \left( \omega t \right) \right]\)
La corrente elettrica nella spira si ottiene attraverso la legge di Ohm:
\(i(t)=\frac{fem}{R}=\frac{7{{B}_{0}}\ \omega }{20R}\left[ \cos \left( \omega t \right)+\sin \left( \omega t \right) \right]\,{{e}^{-\omega t}}\)
La corrente cambia verso quando \(\cos \left( \omega t \right)+\sin \left( \omega t \right)=0\) . Per la prima volta si ha quando \(\omega t=\frac{3\pi }{4}\) \(\Rightarrow \) \(t=\frac{3\pi }{4\omega }\)
Soluzione Quesito 1 – Simulazione Seconda prova Maturità scientifica 2 Aprile 2019
La funzione in base al suo dominio, ha un potenziale asintoto verticale in x=1 ed uno orizzontale o obliquo per \(x\to \pm \infty\)
\(\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{\left( k-1 \right){{x}^{3}}+k{{x}^{2}}-3}{x-1}=\frac{\infty }{\infty }\,\) \(\,\overset{H}{\mathop{=}}\,\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{3\left( k-1 \right){{x}^{2}}+2kx}{1}=\pm \infty \) se \(k\ne 0\) \(\Rightarrow\). Sotto la condizione \(k\ne 0\) possiamo affermare che non ci sono asintoti orizzontali
\(\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{g(x)}{x}=\) \(\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{\left( k-1 \right){{x}^{3}}+k{{x}^{2}}-3}{{{x}^{2}}-x}=\frac{\infty }{\infty }\,\) \(\,\overset{H}{\mathop{=}}\,\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{3\left( k-1 \right){{x}^{2}}+2kx}{2x-1}=\frac{\infty }{\infty }\,\) \(\,\overset{H}{\mathop{=}}\,\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{6\left( k-1 \right)x+2k}{2}=\pm \infty \) se \(k\ne 1\) \(\Rightarrow \) Sotto la condizione \(k\ne 1\) possiamo affermare che non ci sono asintoti obliqui
Per evitare l’asintoto verticale in x=1, dobbiamo cercare un valore di k tale che il numeratore risulta divisibile per il denominatore e quindi dobbiamo fare in modo che x=1 sia una radice del numeratore’:
posto \(h(x)=\left( k-1 \right){{x}^{3}}+k{{x}^{2}}-3\) \(\Rightarrow\) \(h(1)=\left( k-1 \right)+k-3=0\) \(\Rightarrow \) \(k=2\)
Posto k=2, che rispetta anche le condizioni \(k\ne 0\) e \(k\ne 1\) si ha che in x=1, non ci sarà un asintoto verticale ma una discontinuità di terza specie.
\(\underset{x\to 1}{\mathop{\lim }}\,\frac{{{x}^{3}}+2{{x}^{2}}-3}{x-1}=\frac{0}{0}\,\,\overset{H}{\mathop{=}}\,\underset{x\to 1}{\mathop{\lim }}\,\frac{3{{x}^{2}}+4x}{1}=7\)
Affinché la funzione presenti un asintoto obliquo si deve avere che il limite per \(x\to \infty \) di \(\frac{g(x)}{x}\) deve essere finito e non nullo.
Posto k=1 si ha:
\(m=\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{g(x)}{x}=\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{{{x}^{2}}-3}{{{x}^{2}}-x}=\frac{\infty }{\infty }\,\) \(\,\overset{H}{\mathop{=}}\,\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{2x}{2x-1}=\frac{\infty }{\infty }\,\) \(\,\overset{H}{\mathop{=}}\,\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{2}{2}=1\)
\(q=\underset{x\to \pm \infty }{\mathop{\lim }}\,g(x)-x=\) \(\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{{{x}^{2}}-3}{x-1}-x=\frac{\infty }{\infty }\,\) \(\,\overset{H}{\mathop{=}}\,\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{-3+x}{x-1}=\frac{\infty }{\infty }\,\,\) \(\overset{H}{\mathop{=}}\,\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{2}{2}=1\)
Con \(k=1\) l’asintoto obliquo è \(y=x+1\)
Soluzione Quesito 2 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
La funzione f(x) è pari e derivabile in \(\mathbb{R}\)
Applico la definizione di funzione pari:
\(f(x)=f(-x)\) \(\forall x\in \mathbb{R}\)
Derivo entrambi i membri rispetto a x. L’uguaglianza continua a valere su tutto \(\mathbb{R}\) essendo f(x) derivabile su tutto l’asse dei reali.
\(\frac{d}{dx}f(x)=\frac{d}{dx}f(-x)\) \(\Rightarrow \) \({f}'(x)=-{f}'(-x)\) e quindi f’è una funzione dispari.
La funzione g(x) è dispari e derivabile in \(\mathbb{R}\)
Applico la definizione di funzione pari:
\(g(x)=-g(-x)\) \(\forall x\in \mathbb{R}\)
Derivo entrambi i membri rispetto a x. L’uguaglianza continua a valere su tutto \(\mathbb{R}\) essendo f(x) derivabile su tutto l’asse dei reali.
\(\frac{d}{dx}g(x)=\frac{d}{dx}\left( -g(-x) \right)\) \(\Rightarrow \) \({g}'(x)={g}'(-x)\) e quindi g’è una funzione pari.
Soluzione Quesito 3 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
Supponiamo di conoscere la primitiva della funzione integranda, ovvero una funzione F(t) derivabile tale che \({F}’\left( t \right)\ =\frac{\cos \left( \frac{\pi }{3}t \right)}{t}\) .
La retta tangente al grafico di f(x) nel punto di ascissa 1 ha equazione:
\(y={f}'(1)(x-1)+f(1)\)
A questo punto procediamo con il calcolo di \(f(1)\) e di \({f}’\left( 1 \right)\).
\(f\left( 1 \right)=\int_{1}^{1}{\ \frac{\cos \left( \frac{\pi }{3}t \right)}{t}}\ dt=0\). perché è l’integrale di una funzione su un intervallo nullo.
\(f’\left( 1 \right)=\underset{h\to 0}{\mathop{\lim }}\,\frac{F(1+h)-F(1)}{h}=\frac{0}{0}\,\) \(\,\overset{H}{\mathop{=}}\,\,\underset{h\to 0}{\mathop{\lim }}\,\frac{F'(1+h)}{1}\) \(=\,\underset{h\to 0}{\mathop{\lim }}\,\frac{\cos \left( \frac{\pi }{3}\left( 1+h \right) \right)}{1+h}\) \(=\cos \left( \frac{\pi }{3} \right)=\frac{1}{2}\)
Quindi la retta tangente ha equazione: \(y=\frac{1}{2}(x-1)\)
Soluzione Quesito 4 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
Sia il vettore \({{\vec{v}}_{AB}}=B-A=(2,2,0)\)
La retta r ha equazioni parametriche date da \(r\left( t \right)={{\vec{v}}_{AB}}\cdot t+A\):
$$ r:\left\{ \begin{align*} & x=2t-2 \\ & y=2t \\ & z=1 \end{align*} \right. $$
Devo cercare un punto P appartenente alla retta r, equidistante da C e da D:
\(PC=PD\) \(\Rightarrow\) \(P{{C}^{2}}=P{{D}^{2}}\)
L’espressione del punto P in funzione di t è P(t)=(2t-2, 2t, 1). Applico la formula per la distanza tra due punti e ottengo la seguente equazione:
\({{\left( 2t-2-5 \right)}^{2}}+{{\left( 2t-1 \right)}^{2}}+{{\left( 1+2 \right)}^{2}}=\) \({{\left( 2t-2-1 \right)}^{2}}+{{\left( 2t-3 \right)}^{2}}+{{\left( 1-4 \right)}^{2}}\)
Semplificando si ottiene un’equazione di primo grado la cui soluzione è t=4, per cui il punto cercato è P(4)=(6, 8, 1)
Soluzione Quesito 5 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
Qual è la probabilità che, dopo 4 lanci, il suo punteggio sia ancora 0?
L’unico modo per ottenere 0 in 4 lanci è che esce una sola volta 3 e le restanti 3 volte numeri diversi da 3. Quindi la probabilità cercata è, la probabilità di ottenere una sola volta 3 in 4 lanci di dadi:
$$ P=\begin{pmatrix} 4 \\ 1 \end{pmatrix}p(1-p)^3=38.6\% $$
Con $ p=\frac{1}{6} $, $ 1-p=\frac{5}{6} $ e il coefficiente binomiale vale:
$$ \begin{pmatrix} 4 \\ 1 \end{pmatrix}=\frac{4!}{1!3!}=4 $$
Qual è la probabilità che, in una sequenza di 6 lanci, il punteggio non scenda mai sotto lo 0?
Perché il punteggio non scenda mai sotto lo zero si deve avere che esce 3 al primo lancio e almeno un altro 3 nei quattro lanci successivi
Detto X=”numero di volte che esce 3 tra il secondo e il quinto lancio”, la probabilità cercata è:
\(P=p\cdot \Pr (X\ge 1)=p\cdot \left[ 1-\Pr (X<1) \right]=\) \(p\cdot \left[ 1-\Pr (X=0) \right]=\) \(\frac{1}{6}\left[ 1-{{\left( \frac{5}{6} \right)}^{4}} \right]=\) \(\frac{{{6}^{4}}-{{5}^{4}}}{{{6}^{5}}}=8,63\%\)
Soluzione Quesito 6 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
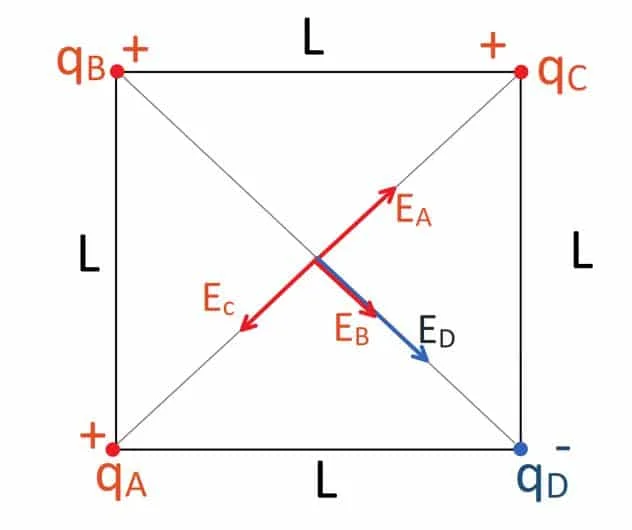
I campi elettrici al centro del quadrato sono rappresentati in figura, dove si è tenuto conto del segno delle cariche (l’unica negativa che genera un campo diretto verso di se è la carica posta nel vertice D)
Osservando che la distanza di ciascun vertice dal centro del quadrato può essere calcolata attraverso il teorema di Pitagora \(d=\frac{L}{\sqrt{2}}\) calcoliamo i moduli dei vari campi elettrici attraverso il :
\({{E}_{A}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{{{q}_{A}}}{d}\), \({{E}_{B}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{{{q}_{B}}}{d}\), \({{E}_{C}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{{{q}_{C}}}{d}\) , \({{E}_{D}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{{{q}_{D}}}{d}\)
Per ottenere le componenti dei vari campi elettrici lungo l’asse x e lungo l’asse y, moltiplichiamo rispettivamente per \(\cos 45\) e per \(\sin 45\).
\(\cos 45=\sin 45=\frac{1}{\sqrt{2}}\)
Il campo elettrico lungo l’asse x vale:
\({{E}_{x}}=\frac{{{E}_{A}}}{\sqrt{2}}+\frac{{{E}_{B}}}{\sqrt{2}}-\frac{{{E}_{C}}}{\sqrt{2}}+\frac{{{E}_{D}}}{\sqrt{2}}=\) \(\frac{1}{4\pi {{\varepsilon }_{0}}d\sqrt{2}}\left( {{q}_{A}}+{{q}_{B}}-{{q}_{C}}+{{q}_{D}} \right)=\) \(\frac{1}{4\pi {{\varepsilon }_{0}}L}\left( {{q}_{A}}+{{q}_{B}}-{{q}_{C}}+{{q}_{D}} \right)\)
Il campo elettrico lungo l’asse y vale:
\({{E}_{y}}=\frac{{{E}_{A}}}{\sqrt{2}}-\frac{{{E}_{B}}}{\sqrt{2}}-\frac{{{E}_{C}}}{\sqrt{2}}-\frac{{{E}_{D}}}{\sqrt{2}}=\) \(\frac{1}{4\pi {{\varepsilon }_{0}}L}\left( {{q}_{A}}-{{q}_{B}}-{{q}_{C}}-{{q}_{D}} \right)\)
Il modulo del campo elettrico è dato da \(E=\sqrt{{{E}_{x}}^{2}+{{E}_{y}}^{2}}\)
La direzione è individuata dall’angolo \(\theta ={{\tan }^{-1}}\frac{{{E}_{y}}}{{{E}_{x}}}\)
Soluzione Quesito 7 – Simulazione Seconda prova maturità scientifica 2 aprile 2019
Un protone di massa \({{m}_{p}}\) e carica \({{q}_{p}}\) viene accelerato da una d.d.p. di 400V quindi raggiunge la velocità \({{v}_{p}}\) che manterrà per tutto il tragitto, poiché il campo magnetico ha la proprietà di deviare la traiettoria ma non modificare la velocità. Il campo di induzione magnetica infatti esercita sul protone una forza ortogonale alla velocità, che determina un’accelerazione centripeta. La forza è costante, quindi il protone si muove all’interno del campo magnetico di moto circolare uniforme.
La velocità \({{v}_{p}}\) può essere calcolata mediante la conservazione dell’energia:
\({{q}_{p}}V=\frac{1}{2}{{m}_{p}}{{v}_{p}}^{2}\) \(\Rightarrow\) \({{v}_{p}}=\sqrt{\frac{2{{q}_{p}}V}{{{m}_{p}}}}\)
La forza centripeta è data dalla forza di Lorentz \(\vec{F}=q{{\vec{v}}_{p}}\times \vec{B}\) e poiché la velocità e il campo di induzione magnetica sono perpendicolari, l’espressione per il modulo della forza diventa \(F=q{{v}_{p}}B\). Per la seconda legge di Newton la forza e l’accelerazione (centripeta) sono legate da \(F=ma\) \(\Rightarrow \) \(a=\frac{F}{{{m}_{p}}}=\frac{q{{v}_{p}}B}{{{m}_{p}}}\) . In un moto circolare l’accelerazione centripeta è legata al raggio della traiettoria dalla relazione \(a=\frac{{{v}_{p}}^{2}}{R}\) .
Uguagliando le due espressioni dell’accelerazione centripeta ottenuta si ha che
\(\frac{q{{v}_{p}}B}{{{m}_{p}}}=\frac{{{v}_{p}}^{2}}{R}\) \(\Rightarrow \) \(B=\frac{{{m}_{p}}{{v}_{p}}}{{{q}_{p}}{{v}_{p}}R}\)
Il raggio della traiettoria può essere ricavato dal grafico e vale \(R=\sqrt{2}\).
