Indice dei contenuti
- PROBLEMA 1
- PROBLEMA 2
- QUESTIONARIO
- SOLUZIONE PROBLEMA 1
- SOLUZIONE PROBLEMA 2
- SOLUZIONE QUESITI
- Soluzione quesito 1 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
- Soluzione quesito 2 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
- Soluzione quesito 3 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
- Soluzione quesito 4 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
- Soluzione quesito 5 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
- Soluzione quesito 6 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
- Soluzione quesito 7 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
- Soluzione quesito 8 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
PROBLEMA 1
Hai giocato con il tuo fratellino con un trenino elettrico da lui ricevuto in regalo per il compleanno. Osservandolo, più volte ti sei chiesto quale sia il principio di funzionamento delle varie parti. In particolare hai osservato che quando un vagone viene immesso in un binario morto, nei pressi del respingente finale il vagone subisce un forte rallentamento fino quasi a fermarsi; questo consente al vagone di raggiungere il respingente finale con velocità molto bassa e quindi di colpirlo senza conseguenze.
Per capire il funzionamento di questo freno, hai analizzato in dettaglio il binario morto e un vagone; hai notato che sulla parte finale del binario morto è presente un piccolo magnete permanente di forma quadrata di lato $𝐿=5,0𝑐𝑚$ fissato tra le due rotaie del binario. Inoltre sul fondo del vagone è presente una cornice quadrata di dimensione uguale al magnete su cui è avvolto un filo a formare una spira quadrata di resistenza elettrica $𝑅=0,020Ω.$ Analizzando il moto del vagone hai compreso che quando il vagone passa sopra il magnete, anche la spira passa sopra il magnete (come mostrato in figura) e che in questo passaggio il vagone rallenta.
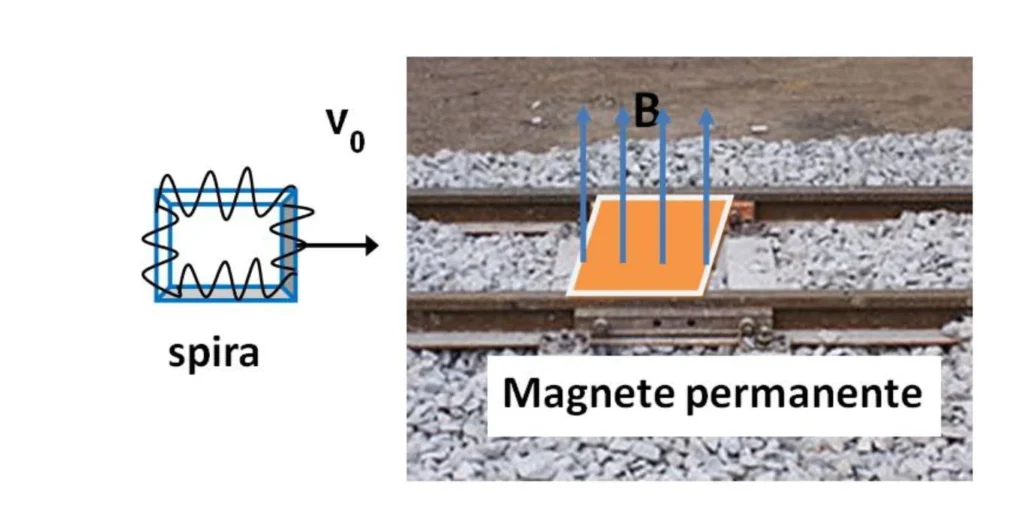
1. Spiega qualitativamente l’origine della azione frenante dovuta al passaggio della spira sopra al magnete.
2. Assumendo che il magnete permanente generi sopra di sé un campo magnetico $𝐵=0,85𝑇$ uniforme, perpendicolare al magnete stesso (e quindi anche alla spira) e trascurando tutti gli effetti di bordo, dimostra che l’equazione del moto della spira durante il passaggio sul magnete è:
$$𝑚\frac{𝑑𝑣}{𝑑𝑡}=−\frac{𝐵^2𝐿^2}{𝑅}𝑣 $$
dove $𝑚=50𝑔$ è la massa del vagone.
3. Verifica che l’equazione del moto ha come soluzione $v = v_0 \cdot e^{-\frac{t}{\tau}}$ dove $v_0$ è la velocità del vagone (e quindi della spira) quando entra nel campo del magnete permanente, esprimendo la costante $\tau$ in termini delle altre grandezze presenti nell’equazione del moto e calcolandone il valore numerico.
4. Assumendo per la velocità iniziale il valore $v_0 = 0.20 \frac{m}{s}$, determina il tempo che la spira impiega ad attraversare completamente il magnete e la velocità che essa ha dopo aver attraversato il magnete.
5. Dimostra che se la velocità iniziale $v_0$ è inferiore ad un valore limite, la spira non riesce a superare il magnete permanente: in queste condizioni il freno agisce.
Clicca per leggere la svolgimento
PROBLEMA 2

Il 14 ottobre 2012 Felix Baumgartner ha realizzato un lancio storico ottenendo tre record mondiali:
– la maggiore altezza raggiunta da un uomo in una ascesa con un pallone ($39045 m$);
– il lancio più alto in caduta libera;
– la più alta velocità in caduta libera ($1341,9 km/h$).
Dopo l’ascesa in un pallone gonfiato a elio, si è lanciato verso la Terra, protetto da una tuta speciale, e ha aperto il suo paracadute dopo 4 minuti e 20 secondi di caduta libera. Il lancio è durato in totale 9 minuti e 3 secondi.
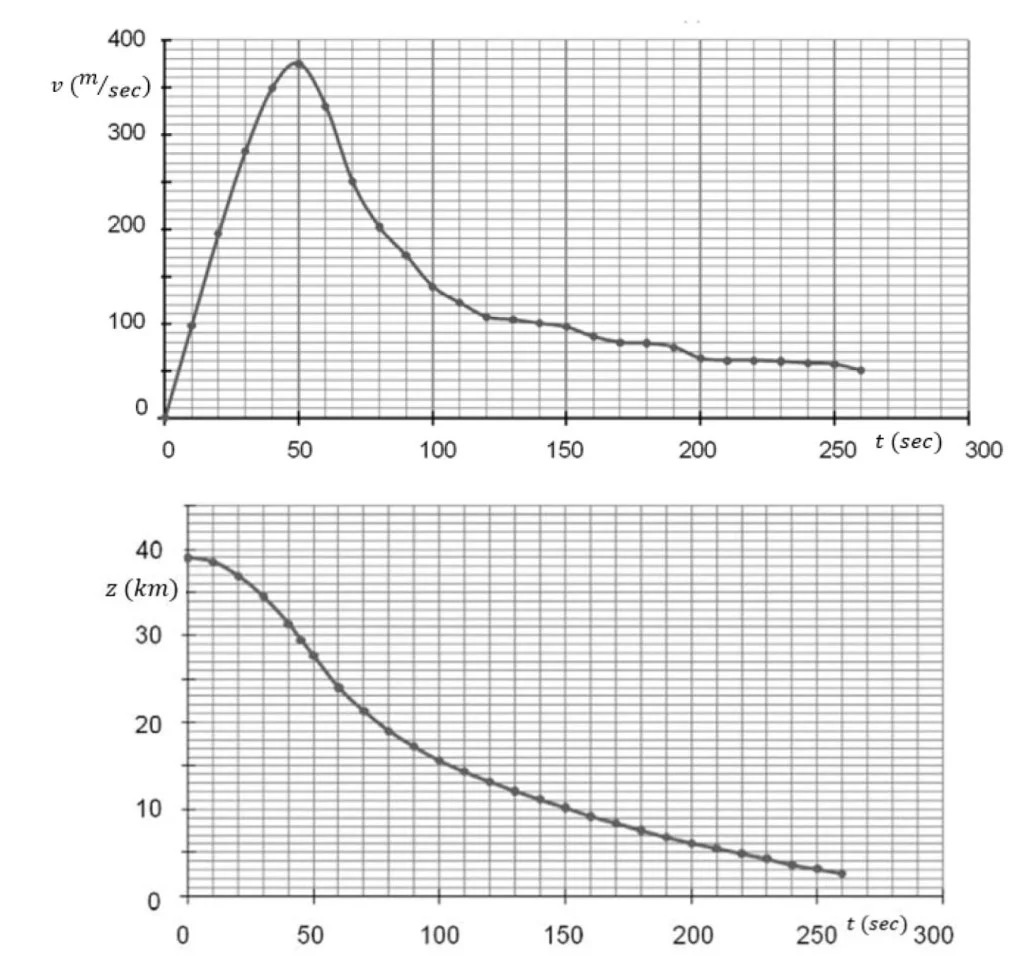
Nelle figure seguenti sono riportati gli andamenti della velocità e della quota di Baumgartner durante il lancio, a partire dall’istante del lancio $t=0$.
Per realizzare l’ascesa è stato necessario utilizzare un enorme pallone deformabile: ciò per fare in modo che all’aumentare della quota e al diminuire della densità dell’aria il volume del pallone possa aumentare, mantenendo così costante la spinta verso l’alto (spinta di Archimede). Su un giornale veniva riportato “Per assicurare una velocità d’ascesa sufficiente la spinta verso l’alto era circa doppia di quella necessaria per tenere in equilibrio il sistema. In pratica, aggiungendo alla massa di Baumgartner quella del pallone riempito ad elio, era necessario sollevare una massa di circa 3 tonnellate”. La massa di Baumgartner e della sua tuta è pari a circa $120 kg$.
Fase di ascesa
1. Disegna il diagramma delle forze subito dopo il decollo, trascurando la forza di attrito. Non è necessario che il disegno sia in scala, deve però essere coerente con la situazione fisica.
2. Dopo qualche minuto di ascensione il moto può essere considerato rettilineo uniforme. In questa situazione, calcola approssimativamente il valore della forza di attrito con l’aria.
Fase di lancio
Scegli un sistema di riferimento e studia la caduta verticale del sistema S costituito da Baumgartner e dalla tuta. In questa fase, si può ritenere trascurabile l’effetto della spinta di Archimede.
3. Utilizzando i grafici, determina l’accelerazione di S per $t<20s$ e commenta il risultato ottenuto.
4. Il sistema $S$ ha raggiunto velocità supersoniche durante la caduta? Tieni presente la seguente tabella, che riporta la velocità del suono in aria ad altezze diverse:
| Altezza (km) | 10 | 20 | 30 | 40 |
| Velocità del suono (m/s) | 305 | 297 | 301 | 318 |
5. Calcola la variazione di energia meccanica $\Delta{E_m}$ tra il momento in cui Baumgartner salta e il momento in cui raggiunge la massima velocità; fornisci la tua interpretazione del risultato.
6. Nella figura seguente vengono riportati i diagrammi delle forze applicate al sistema S durante la fase di lancio. \(\overrightarrow{P}\)rappresenta la forza peso e \(\overrightarrow{𝑓}\) la forza di attrito con l’aria. Poni in corrispondenza i diagrammi con i tre istanti \(𝑡_1=40𝑠\),\(𝑡_2=50𝑠\),\(𝑡_3=60𝑠\).

7. Determina a quale altitudine Baumgartner ha aperto il paracadute. Ricordando che il lancio è durato in totale 9 minuti e 3 secondi, calcola la velocità media di discesa dopo l’apertura del paracadute, fino all’arrivo al suolo. Ti appare ragionevole considerare il moto in quest’ultima fase come un moto rettilineo uniforme?
8. Per valutare il rischio di traumi derivanti dall’impatto dell’arrivo al suolo, fornisci una stima dell’altezza da cui Baumgartner sarebbe dovuto saltare, senza paracadute, per giungere al suolo con la stessa velocità.
Clicca per leggere la svolgimento
QUESTIONARIO
QUESITO 1
Una spira a forma di parabola di equazione $y = a \cdot x^2$ è immersa in un campo magnetico uniforme $B$ perpendicolare al piano $xy$ della parabola. All’istante $t = 0$ una barretta inizia a traslare lungo la parabola partendo dal suo vertice con accelerazione costante come indicato in figura. Determinare la forza elettromotrice indotta sulla spira in funzione della $y$.
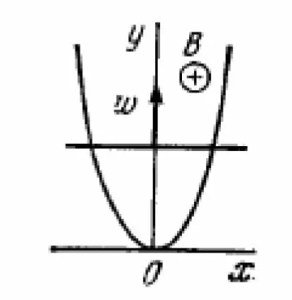
QUESITO 2
La posizione di una particella varia con il tempo secondo l’equazione:
$$ x = \alpha t(1 – \beta t) $$
dove $ \alpha $ e $ \beta $ sono due costanti, con $ \beta > 0 $.
Determina:
a) la velocità e l’accelerazione della particella in funzione del tempo;
b) l’intervallo di tempo necessario alla particella, che parte dall’origine, per ritornare nell’origine e lo spazio percorso in questo intervallo di tempo.
QUESITO 3
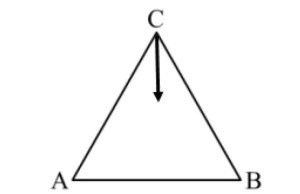
Tre cariche puntiformi di valore q sono poste ai vertici del triangolo equilatero $ABC$, i cui lati
misurano $1m$.
a) Determina l’energia potenziale del sistema.
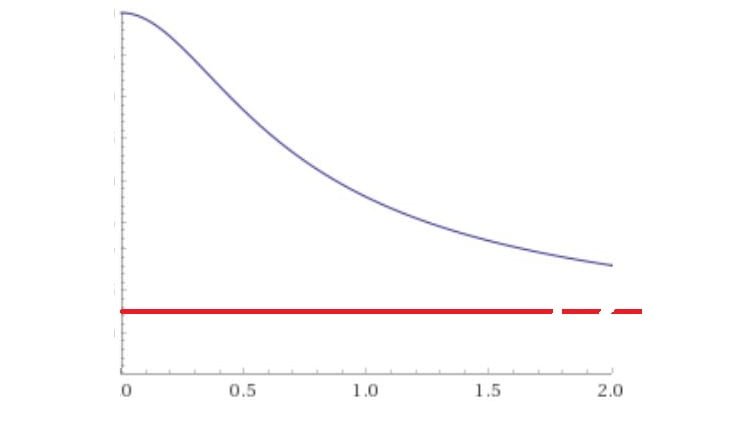
b) La carica collocata in $C$ viene spostata verso il segmento $AB$ lungo la perpendicolare ad $AB$; traccia il grafico dell’andamento dell’energia potenziale del sistema in funzione della distanza della carica dal segmento $AB$.
QUESITO 4
Un punto materiale si muove nel piano $xy$ secondo la legge oraria:
$$ x = a \cdot \sin(\omega t), \quad y = a(1 – \cos(\omega t)), $$
con $a$ e $\omega$ costanti positive. Determina la distanza del punto dall’origine al tempo $t = \tau$ e le direzioni dei vettori velocità e accelerazione all’istante $t = 0$.
QUESITO 5
Un elettrone si muove, partendo da fermo, in un campo elettrico uniforme di intensità $E=10kV/cm$. Descrivi il procedimento che adotteresti per determinare l’istante in cui l’energia cinetica dell’elettrone sarà uguale alla sua energia a riposo.
QUESITO 6
Quanto tempo impiegherà un’onda sonora a percorrere la distanza $l$ tra i punti A e B se la temperatura dell’aria tra di essi varia linearmente da $T_1$ a $T_2$? Tieni presente che la velocità di propagazione nell’aria varia in funzione della temperatura secondo la legge:
$$ v = a \cdot \sqrt{T} $$
dove $a$ è una costante.
QUESITO 7
Il grafico riportato nella figura seguente potrebbe rappresentare l’andamento della velocità con cui una carica puntiforme si allontana per repulsione elettrostatica da un’altra carica puntiforme, fissa, di eguale segno? Motiva la tua risposta.
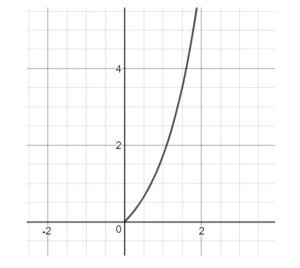
QUESITO 8
Un punto si muove lungo l’asse $x$ secondo la legge:
$$ x = a \cdot \sin^2(3t – \frac{\pi}{4}) $$
con $a$ costante positiva. Determina:
a) l’ampiezza e il periodo di oscillazione;
b) l’istante $t$ in cui il punto raggiunge per la prima volta la massima distanza dall’origine.
Clicca per le altre simulazioni per la maturità scientifica.
SOLUZIONE PROBLEMA 1
Soluzione prima domanda
Nella spira, man mano che essa entra nella regione dove è presente il campo magnetico, varia il flusso del campo magnetico attraverso di essa, quindi, come garantito dalla Legge di Faraday, si genera una fem indotta che fa rallentare la spira e il vagone ad essa collegato. Quindi l’origine dell’azione frenante è di natura elettromagnetica. Sulla spira, essendo essa chiusa, circolerà una corrente elettrica il cui verso deve ubbidire alla Legge di Faraday-Newmann-Lenz. La spira-vagone rallenterà perché i lati della spira perpendicolari ai binari subiranno una forza descritta dalla Legge di Laplace (forza agente su un filo percorso da un’intensità di corrente elettrica immerso in un campo magnetico).
Soluzione seconda domanda
In un certo istante di tempo $t$, la superficie della spira immersa nel campo magnetico ha area $\Sigma(t) = L \cdot s(t)$, dove $s(t)$ indica la posizione che occupa il lato più avanzato della spira all’istante $t$.
Poiché $fem(t) = -\frac{d\Phi_B (t)}{dt}$, allora si ha che $fem(t) = -\frac{d(B \cdot Ls(t))}{dt}$. Derivando rispetto al tempo si ha: $fem(t) = -B \cdot L \cdot \frac{ds(t)}{dt}$ ed infine $fem(t) = -BLv(t)$.
Nella spira circolerà una corrente $i(t)$ che può essere calcolata in base alla prima Legge di Ohm:
$$i(t) = \frac{fem(t)}{R} = -\frac{BLv(t)}{R}$$
La forza di natura elettromagnetica indotta sulla spira è descritta dalla Legge di Laplace $\overrightarrow{F}(t) = i(t) \cdot \overrightarrow{L} \times \overrightarrow{B}$, da cui si ha che:
$$F(t) = -\frac{B^2L^2}{R}v(t)$$
Per il secondo Principio della dinamica ottengo:
$$m \cdot a(t) = -\frac{B^2L^2}{R} \cdot v(t) \Rightarrow m \cdot \frac{dv(t)}{dt} = -\frac{B^2L^2}{R}v(t)$$
dove con $a(t)$ abbiamo indicato l’accelerazione della spira nell’istante di tempo $t$.
Soluzione terza domanda
Si tratta di risolvere un’equazione differenziale a variabili separabili
$mv′ = − \frac{B^2 L^2}{R}\cdot v$ $\Rightarrow$ $\frac{v′}{v}= − \frac{B^2L^2}{m\cdot R}$ $\Rightarrow$ $ln \left|v \right| = −\frac{B^2L^2}{m \cdot R} t + c , \, c ∈ \mathbb{R}- \left \{ 0\right \}$ $\Rightarrow$ $v = ±e^c \cdot e^{− \frac{B^2L^2}{mR}\cdot t}$ $\Rightarrow$ $v = k·e^{\frac{− B^2L^2}{mR}t}$,$k ∈\mathbb{R}$\{0}.
Poiché v = 0 è soluzione particolare, la soluzione generale dell’equazione differenziale è
$v = k·e^{− \frac{B^2L^2}{m\cdot R} t}$ con $k ∈\mathbb{R}$/{0}.
Poiché $v(0) = v_0$ , ottengo $k = v_0$ per cui il problema di Cauchy
$\left\{\begin{matrix} mv′ = − \frac{B^2 L^2}{R}\cdot v \\ v(0)=v_0 \end{matrix}\right.$
ammette come soluzione $v = v_0·e^{− \frac{B^2L^2}{m\cdot R} t}$. Posto $\frac{m\cdot R}{B^2L^2} = τ $, posso riscrivere la soluzione nella forma attesa, ovvero $v = v_0\cdot e^{−\frac{t}{τ}}$.
Per finire calcoliamo il valore numerico di τ:
$τ=\frac{m\cdot R}{B^2L^2} = \frac{5,0·10^{−2} \cdot 2,0\cdot 10^{−2}}{0,85^2 \cdot (5,0 \cdot 10^{ −2 })^2 }= 0,55 s$ .
Soluzione quarta domanda
Dal punto precedente abbiamo calcolato la legge oraria della velocità. Per rispondere a questa domanda occorre calcolare la legge oraria dello spazio. Per fare ciò possiamo ricavare il problema di Cauchy a partire dalla velocità ricordando che essa è la derivata rispetto al tempo dello spazio $v = s’$:
$$\left\{\begin{matrix}s’ = v = v_0 \cdot e^{-\frac{t}{\tau}} \\s(0) = 0\end{matrix}\right.$$
La soluzione si ottiene integrando entrambi i membri della prima equazione:
$$\int ds = \int v_0 \cdot e^{-\frac{t}{\tau}} dt \Rightarrow s = -\tau \cdot v_0 \cdot e^{-\frac{t}{\tau}} + c, \, c \in \mathbb{R}$$
Poiché $s(0) = 0$ si ha che $c = v_0 \tau$, e la funzione che risolve il problema di Cauchy è $s(t) = v_0 \tau (1 – e^{-\frac{t}{\tau}})$. La spira attraverserà completamente il magnete quando $s(\overline{t}) = 2L$, in corrispondenza dell’istante temporale $\overline{t}$ che si ottiene risolvendo l’equazione e vale $\overline{t} = 1.3s$.
La velocità di uscita del vagone è la velocità all’istante $\overline{t}$, ovvero $v(1.3) = 0.019 \, \text{m/s}$.
Soluzione quinta domanda
La velocità limite si ha quando in un tempo infinito lo spazio percorso è esattamente pari a $2L$, quindi bisogna imporre che $\underset{t \to \infty}{\lim} s(t) = 2L$ $\Rightarrow$ $\underset{t \to \infty}{\lim} v_{\text{lim}} \tau (1 – e^{-\frac{t}{\tau}}) = v_{\text{lim}} \tau = 2L$
Da cui $v_{\text{lim}} = \frac{2L}{\tau} = 0.18 \, \text{m/s}$
SOLUZIONE PROBLEMA 2
Soluzione prima domanda
L’utilizzo del pallone deformabile suggerisce che la spinta di Archimede \(\overrightarrow{F_A}\) sia costante; inoltre anche la forza peso pallone-Baumgartner con tuta \(\overrightarrow{F_P}\) è costante; necessariamente \(F_P ≤F_A \), altrimenti il tutto non si alzerebbe. Trascurando l’attrito con l’aria non ci sono altre forze in gioco in questa fase e lo schema delle forze è come quello in figura.
Soluzione seconda domanda
La massa totale è m= 3,0·103 kg , quindi \(F_P = m\cdot g = 2,29·10^4 N\) , dove g indica l’accelerazione di gravità.
Per l’equilibrio si dovrebbe avere \(F_A = F_P +R \), dove \(\overrightarrow{R}\) indica la forza di attrito dell’aria. La spinta verso l’alto era circa doppia di quella necessaria per tenere in equilibrio il sistema (trascurando l’attrito), quindi \(F_A = 2F_P = 5,88\cdot 10^4 N\) , per cui \(\overrightarrow{R}=\overrightarrow{F_P}\)
Soluzione terza domanda
Scelgo come sistema di riferimento una retta orientata verso il centro della terra con lo zero posto nel punto nel quale il grave inizia il lancio. Inizialmente, nei primi trenta secondi, il diagramma v-t è approssimabile a una retta (Moto Rettilineo Uniformemente Accelerato); alla fine, da 120 s, approssimativamente il diagramma s-t è approssimabile a una retta (moto Rettilineo Uniforme). Tra i due intervalli il moto è accelerato (non in modo uniforme) fino a raggiungere (o avvicinandosi)
alla velocità limite (all’istante t= 50 s ), subito dopo Baumgartner presumibilmente si dispone in modo tale da far aumentare la superficie esposta alla direzione dell’aria e compie un moto decelerato (non uniforme).
L’accelerazione media nei primi venti secondi vale \(a = \left | \frac{Δv}{Δt} \right |= \left | \frac{200−0}{20−0} \right |=10m/ s^2 \).
Soluzione quarta domanda
Incrociando le due leggi orarie riportate graficamente nella traccia è possibile costruire una tabella s-v:
| Altezza (km) | 10 | 20 | 30 | 40 |
| Velocità di Felix (m/s) | 100 | 220 | 360 | 0 |
Si ha che la risposta è si, il sistema ha superato la velocità del suono tra i 40 s e i 60 s.
Soluzione quinta domanda
Sia \(m_B\) la massa del grave (Felix + tuta). Stimo l’altezza da terra all’istante in cui raggiunge la massima velocità come 28˙000 metri.
\(E_i = m_B\cdot g\cdot h_i = 4,59·107 J \);
\(E_f = m_B\cdot g\cdot h_f + \frac{1}{2}m_Bv_{MAX}^2 = 4,13·10^7 J \).
Quindi la variazione di energia meccanica è pari a \(ΔE_m =E_f −E_i =−4,65·10^6 J\) . Tale differenza di energia è stata dissipata sotto forma di calore generato dall’attrito dell’aria con il grave.
Soluzione sesta domanda
L’attrito viscoso dell’aria è direttamente proporzionale alla velocità del grave, quindi a parità della forma del grave, maggiore è la velocità maggiore sarà f; all’istante \(t_2\) Baumgartner si dispone in modo da aumentare la superficie esposta all’aria e la velocità comincia a diminuire perciò f sarà maggiore perché la forma del grave è tale da aumentare l’attrito con l’aria. Dunque:
- il diagramma A è associato all’istante in cui Baumgartner ha un’elevata velocità e paracadute aperto, ovvero a \(t_3\) ;
- il diagramma B è associato all’istante in cui Baumgartner non ha un’elevata velocità e paracadute chiuso, ovvero a \(t_1\) ;
- il diagramma C è associato all’istante in cui Baumgartner ha un’elevata velocità e paracadute chiuso, ovvero a \(t_2\) .
Soluzione settima domanda
Poiché il moto di caduta libera è durato 260 s, l’apertura del paracadute è avvenuta nell’istante t= 260 s in cui Baumgartner raggiunge la velocità di 50 m/s=180 km/h , a un’altezza da terra di circa 2000 m.
\(\overline{v} = \left | \frac{Δs}{Δt} \right |= \left | \frac{0−2000}{543−260} \right |=7,07 m/s= 25,4 km/h \).
Non è ragionevole considerare la velocità costante in quest’ultima fase, visto che varia dai 50 m/s a 0 m/s. È senz’altro più ragionevole pensare il moto finale come rettilineo uniformemente decelerato con accelerazione media
\(\overline{a} = \left | \frac{Δv}{Δt} \right |= \left | \frac{0−50}{543−260} \right |=1,77 \cdot 10^-1 m/s^2 \).
Se si tiene conto che nella fase di discesa con paracadute, dopo un certo intervallo di tempo il grave raggiunge la velocità limite, da quell’istante in poi ha senso considerare il moto rettilineo uniforme. In tal caso lo schema delle forze dà
\(−m_B \cdot a =−R+F_P \) \(\Rightarrow\) \(−m_B v′=−kv+m_B g\) \(\Rightarrow\) \(v′− \frac{k}{m_B}v=-g\) \(\Rightarrow\) \(v=-\frac{m_B}{k}(k’-g e^{\frac{-kt}{m_B}}) \) con \(k’\in \mathbb{R}\)
dove R= kv è il modulo dell’attrito viscoso. Considerando la condizione al contorno v(0)= 50 m/s , ottengo che \(k′=k·\frac{v(0)}{m_B} +g\), da cui \(v(t)= v(0)−τ g (1−e^{ −t τ })\), dove \( τ = \frac{m_B}{k} \) .
La velocità limite si raggiunge dopo un tempo stimato in 4τ ed è pari a \(v(0)+τg\) . Quindi da (260+4τ) s a 543 s è ragionevole considerare il moto rettilineo uniforme.
Soluzione ottava domanda
Trascurando la spinta di Archimede e l’attrito con l’aria, posso considerare il sistema privo di forze non conservative e quindi posso applicare il principio di conservazione dell’energia meccanica. Ottengo che \(m_B g h= \frac{1}{2} m_B (v(0)−τ g)^2 \) \(\Rightarrow\) \(h= \frac{(v(0)−τ g)^2}{2g}\).
Stimando τ = 5 s , trovo k = 24 k/s e quindi il paracadutista arriva a terra con una velocità di 1 m/s . Perciò h= 5,10 cm.
SOLUZIONE QUESITI
Soluzione quesito 1 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
Senza dubbio la sbarretta forma un circuito chiuso con l’arco di parabola sottostante.
Il campo magnetico è uniforme, ma per effetto della traslazione della sbarretta si ha una variazione della superficie compresa tra la sbarretta e l’arco di parabola S(t) e di conseguenza una variazione di flusso magnetico che indurrà lungo la spira una forza elettromotrice come previsto dalla legge di Faraday-Newmann-Lenz.
\[fem=-\frac{d{{\phi }_{B}}}{dt}\]
Il flusso magnetico attraverso la superficie della spira vale: \({{\phi }_{B}}=S(t)B\) essendo il campo magnetico perpendicolare alla spira.
\(S(t)=2y(t)x(t)-\int\limits_{-x(t)}^{x(t)}{a\,{{\left[ x(t) \right]}^{2}}dx}=2y(t)x(t)-2a\,\frac{{{\left[ x(t) \right]}^{3}}}{3}\)
A questo punto tenendo presente che $y=a{{x}^{2}}$ e siccome vogliamo scrivere tutto in funzione di y, si ha che \(x=\sqrt{\frac{y}{a}}\) e sostituendo nell’espressione della superficie
\(S(t)=2y(t)\sqrt{\frac{y(t)}{a}}-\,\frac{2}{3}y(t)\sqrt{\frac{y(t)}{a}}=\frac{4}{3\sqrt{a}}{{\left[ y(t) \right]}^{3/2}}\)
Ritornando alla fem indotta nella spira:
\(fem=-\frac{d{{\phi }_{B}}}{dt}=-\frac{d}{dt}\left( \frac{4}{3\sqrt{a}}{{\left[ y(t) \right]}^{3/2}}B \right)=-\frac{4}{3\sqrt{a}}\frac{3}{2}{{\left[ y(t) \right]}^{1/2}}y'(t)B=-\frac{2B}{\sqrt{a}}\sqrt{y(t)}\,y'(t)\)
Notando che la derivata rispetto al tempo di y(t) rappresenta la velocità della sbarretta, possiamo finalmente scrivere la forza elettromotrice indotta nella spira in funzione di y
\[fem(y)=-2B\omega \sqrt{\frac{y}{a}}\]
Soluzione quesito 2 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
a) La velocità e l’accelerazione corrispondono rispettivamente alla derivata prima e alla derivata seconda di x(t)
\(v(t)=x'(t)=\alpha -2\alpha \beta t\)
\(a(t)=x”(t)=-2\alpha \beta \)
b) Ripassa dall’origine quando \(x(t)=0\)
\(0=\alpha t(1-\beta t)\) ammette due soluzioni, una è t=0 che coincide con l’istante iniziale e l’altra è \(t=\frac{1}{\beta }\) che corrisponde con l’istante temporale cercato.
La massima distanza dall’origine viene raggiunta quando la velocità si annulla v(t)=0, ovvero \(0=\alpha -2\alpha \beta t\)\(\Rightarrow\) \(t=\frac{1}{2\beta }\) , da cui ottengo \({{x}_{\max }}=x(\frac{1}{2\beta })=\alpha \frac{1}{2\beta }(1-\beta \frac{1}{2\beta })=\frac{\alpha }{4\beta }\)
Lo spazio percorso è pari a \(d=2{{x}_{\max }}=\frac{\alpha }{2\beta }\)
Osservazione: Si tratta di un moto uniformemente accelerato visto che la legge oraria è un polinomio di secondo grado nella variabile t (ricordando che la legge oraria di un moto uniformemente accelerato è \(x(t)={{x}_{0}}+{{v}_{0}}t+\frac{1}{2}a\,{{t}^{2}}\)) e poteva essere studiato come tale.
Soluzione quesito 3 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
a) \(U=\frac{1}{4\pi {{\varepsilon }_{0}}}\left( \frac{{{q}_{A}}{{q}_{B}}}{\overline{AB}}+\frac{{{q}_{A}}{{q}_{C}}}{\overline{AC}}+\frac{{{q}_{B}}{{q}_{C}}}{\overline{BC}} \right)=\frac{1}{4\pi {{\varepsilon }_{0}}}3{{q}^{2}}\) dove si è considerato che le cariche sono tutte uguali e pari a q e le distanze tra i vertici, sono tutte uguali essendo il triangolo equilatero e unitarie \(\overline{AB}=\overline{AC}=\overline{BC}=1\)
b) Chiamata x la distanza del vertice C dal lato \(\overline{AB}\) come indicato dalla traccia, il triangolo diventa isoscele con \(\overline{AC}=\overline{BC}=\sqrt{{{\left( \frac{1}{2} \right)}^{2}}+{{x}^{2}}}=\frac{1}{2}\sqrt{1+4{{x}^{2}}}\). Per calcolare i due lati uguali del triangolo abbiamo utilizzato il teorema di Pitagora.
\(U=\frac{1}{4\pi {{\varepsilon }_{0}}}\left( \frac{{{q}_{A}}{{q}_{B}}}{\overline{AB}}+\frac{{{q}_{A}}{{q}_{C}}}{\overline{AC}}+\frac{{{q}_{B}}{{q}_{C}}}{\overline{BC}} \right)=\frac{{{q}^{2}}}{4\pi {{\varepsilon }_{0}}}\left( 1+\frac{4}{\sqrt{1+4{{x}^{2}}}} \right)\)
Il grafico richiesto può essere costruito studiando la funzione \(f\left( x \right)=1+\frac{4}{\sqrt{1+4{{x}^{2}}}}\) nell’intervallo \((0,+\infty )\) e osservando che si tratta di una funzione monotona decrescente e che \(\underset{x\to \infty }{\mathop{\lim }}\,f(x)=1\)
Soluzione quesito 4 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
La traccia fornisce le leggi orarie nel piano cartesiano del punto materiale in funzione del tempo. All’istante t=𝜏 abbiamo che
\(x\left( \tau \right)=a\,\sin (\omega \tau ),\,y(\tau )=a(1-\cos (\omega \tau ))\)
La distanza del punto dall’origine degli assi può essere calcolata attraverso il teorema di Pitagora:
\(d=\sqrt{{{x}^{2}}+{{y}^{2}}}=\sqrt{{{\left[ a\,\sin (\omega t) \right]}^{2}}+{{\left[ a\,-a\cos (\omega t) \right]}^{2}}}=a\sqrt{{{\sin }^{2}}(\omega \tau )+1+{{\cos }^{2}}(\omega \tau )-2\cos (\omega \tau )}\)
Da cui considerando che \({{\sin }^{2}}\left( \omega \tau \right)+{{\cos }^{2}}\left( \omega \tau \right)=1\) e che si ha:
\(d=a\sqrt{2-2\cos (\omega \tau )}\)
Per quanto riguarda velocità e accelerazione, calcoliamo prima velocità e accelerazione lungo l’asse x e lungo l’asse y al tempo zero e poi ne calcoliamo la direzione.
\({{v}_{x}}\left( t \right)=x’\left( t \right)=a\omega \cos (\omega t)\) \(\Rightarrow \) \({{v}_{x}}\left( 0 \right)=a\omega \cos (0)=a\omega \)
\({{v}_{y}}\left( t \right)=y’\left( t \right)=a\omega \sin (\omega t)\) \(\Rightarrow \) \({{v}_{y}}\left( 0 \right)=a\omega \sin (0)=0\)
Per la direzione del vettore velocità si ha che \({{v}_{x}}\ne 0\) , \({{v}_{y}}=0\) , quindi la direzione è parallela all’asse x.
\({{a}_{x}}\left( t \right)=v’\left( t \right)=-a{{\omega }^{2}}\sin (\omega t)\) \(\Rightarrow \) \({{v}_{x}}\left( 0 \right)=-a{{\omega }^{2}}\sin (0)=0\)
\({{v}_{y}}\left( t \right)=y’\left( t \right)=a\omega \cos (\omega t)\) \(\Rightarrow \) \({{v}_{y}}\left( 0 \right)=a{{\omega }^{2}}\cos (0)=a{{\omega }^{2}}\)
Per la direzione del vettore accelerazione si ha che \({{a}_{x}}=0\) , \({{a}_{y}}\ne 0\) , quindi la direzione è parallela all’asse y.
Soluzione quesito 5 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
Indichiamo con 𝑚 la massa (a riposo) dell’elettrone, con 𝑒 la carica, con 𝐾 l’energia cinetica e con
\(\gamma =\frac{1}{\sqrt{1-{{\beta }^{2}}}}\) il fattore di Lorentz.
L’energia totale è \(E=\gamma m{{c}^{2}}=m{{c}^{2}}+K\) e, se deve essere \(K=m{{c}^{2}}\), allora si deve avere che \(\gamma =\frac{1}{\sqrt{1-{{\beta }^{2}}}}=2\) e quindi \({{\beta }^{2}}=\frac{3}{4}\)
A questo punto ricordando che il fattore beta è definito come il rapporta tra la velocità del sistema di riferimento solidale con l’elettrone (la velocità dell’elettrone stesso) e la velocità della luce c= 299 792 458 m/s.
\(\beta \equiv \frac{v}{c}\) \(\Rightarrow \) \(v=\frac{\sqrt{3}}{2}c\)
Abbiamo così ottenuto la velocità tale che l’elettrone raggiunga l’energia cinetica uguale alla sua energia a riposo.
Il campo elettrico è costante, quindi esercita una forza costante sull’elettrone e di conseguenza un’accelerazione costante (seconda legge di Newton).
Detta e= −1,60 · 10−19 C la carica dell’elettrone e m= 9,11 · 10−31kg si ha:
\(F=eE\),\(F=ma\) \(\Rightarrow \) \(a=\frac{F}{m}=\frac{eE}{m}\)
A questo punto per ricavare il tempo necessario a raggiungere la velocità \(v=\frac{\sqrt{3}}{2}c\), introduciamo la quantità di moto, che per velocità confrontabili con la luce assume la forma:
\(p=\gamma mv\) .
Inoltre nella seconda legge di Newton, possiamo riscrivere la forza come la derivata rispetto al tempo della quantità di moto \(F=\frac{dp}{dt}=ma\), da cui si ottiene:
\(dp=ma\,dt\)
Integrando entrambi i membri dell’equazione:
\(\int\limits_{0}^{p}{dp}=\int\limits_{0}^{t}{ma\,dt}\) \(\Rightarrow\) \(p=ma\,t\)
E quindi a questo punto possiamo scrivere:
\(p=\gamma mv=ma\,t\)
Semplificando le masse e sostituendo l’espressione dell’accelerazione, della velocità e il fattore di Lorentz, si ha:
\(\frac{eE}{m}t=2\frac{\sqrt{3}}{2}c\) \(\Rightarrow\) \(t=\frac{\sqrt{3}\,mc}{eE}=3ns\)
Soluzione quesito 6 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
La temperatura può essere espressa come una funzione lineare del tempo, ovvero una retta che nell’intervallo temporale che va da \({{x}_{A}}\) a \({{x}_{B}}\) , varia tra T1 e T2
\(T({{x}_{A}})={{T}_{1}}\)
\(T\left( {{x}_{B}} \right)={{T}_{2}}\)
Per cui la legge oraria della temperatura è data dalla seguente espressione:
\(\frac{T(x)-{{T}_{1}}}{{{T}_{2}}-{{T}_{1}}}=\frac{x-{{x}_{A}}}{{{x}_{B}}-{{x}_{A}}}\) \(\Rightarrow\) \(T(x)={{T}_{1}}+\left( {{T}_{2}}-{{T}_{1}} \right)\frac{x-{{x}_{A}}}{{{x}_{B}}-{{x}_{A}}}\)
Indicando con \(\Delta T={{T}_{2}}-{{T}_{1}}\) la variazione di temperatura e con \(\Delta x={{x}_{B}}-{{x}_{A}}\) l’espressione diventa:
\(T(x)={{T}_{1}}+\frac{\Delta T}{\Delta x}\left( x-{{x}_{A}} \right)\)
E la sua derivata \(T’=\frac{\Delta T}{\Delta x}\)
Lo spostamento in termini di differenziali è dato dall’equazione:
\(dx=vdt=a\sqrt{T}dt\) \(\Rightarrow \) \(dt=\frac{dx}{a\sqrt{T}}=\frac{1}{a}{{T}^{-1/2}}\)
Integrando entrambi i membri si ha:
\(\int\limits_{0}^{\Delta t}{dt}=\frac{1}{a}\int\limits_{{{x}_{A}}}^{{{x}_{B}}}{{{\left[ T\left( x \right) \right]}^{-\frac{1}{2}}}dx}\)
Moltiplicando e dividendo il secondo integrale per la derivata di $T(x)$ che è una costante, si ottiene un integrale semimmediato:
\(\Delta t=\frac{1}{a\,T’}\int\limits_{{{x}_{A}}}^{{{x}_{B}}}{{{\left[ T\left( x \right) \right]}^{-\frac{1}{2}}}\cdot T’dx}=\frac{\Delta x}{a\,\Delta T}\left[ \frac{{{T}^{\frac{1}{2}}}}{\frac{1}{2}} \right]_{{{x}_{A}}}^{{{x}_{B}}}=\frac{\Delta x}{a\,\Delta T}\left[ 2\sqrt{T(x)} \right]_{{{x}_{A}}}^{{{x}_{B}}}\)
Quindi:
\(\Delta t=\frac{2\Delta x}{a\,\Delta T}\left( \sqrt{T({{x}_{B}})}-\sqrt{T({{x}_{B}})} \right)\)
A questo punto sostituisco l’espressione di T(x) nell’equazione:
\(\Delta t=\frac{2\Delta x}{a\,\Delta T}\left( \sqrt{{{T}_{2}}}-\sqrt{{{T}_{1}}} \right)=\frac{2\Delta x}{a\left( \sqrt{{{T}_{2}}}+\sqrt{{{T}_{1}}} \right)\,}\)
Nota: si poteva giungere più rapidamente alla conclusione se si integrava rispetto alla temperatura. Per fare ciò si poteva partire osservando che la temperatura è una funzione lineare dello spazio e quindi la sua derivata rispetto allo spazio vale:
\(\frac{dT}{dx}=\frac{\Delta T}{\Delta x}=\frac{{{T}_{B}}-{{T}_{A}}}{{{x}_{B}}-{{x}_{A}}}\) \(\Rightarrow \) \(dx=\frac{\Delta x}{\Delta T}dT\)
A questo punto si legano i differenziali del tempo e dello spazio attraverso l’equazione utilizzata nella soluzione precedente
\(dx=vdt=a\sqrt{T}dt\)
A questo punto sostituendo al differenziale dello spazio, quello della temperatura si ottiene l’equazione
\(\frac{\Delta x}{\Delta T}dT=a\sqrt{T}dt\) \(\Rightarrow \) \(dt=\frac{\Delta x}{\Delta T\,a\sqrt{T}}dT\)
Integrando entrambi i membri si arriva in maniera più elegante alla stessa conclusione di prima:
\(\int\limits_{0}^{\Delta t}{dt}=\frac{\Delta x}{\Delta T\,a}\int\limits_{{{T}_{1}}}^{{{T}_{2}}}{\frac{1}{\sqrt{T}}dT}=\frac{\Delta x}{\Delta T\,a}\left[ 2\sqrt{T} \right]_{{{T}_{1}}}^{{{T}_{2}}}=\frac{2\Delta x}{a\,\Delta T}\left( \sqrt{{{T}_{2}}}-\sqrt{{{T}_{1}}} \right)=\frac{2\Delta x}{a\left( \sqrt{{{T}_{2}}}+\sqrt{{{T}_{1}}} \right)\,}\)
Soluzione quesito 7 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
Nella traccia non è specificato se quello in figura è un grafico della velocità in funzione del tempo o dello spazio. Poiché include l’origine, e poiché fisicamente non è possibile che due cariche partono dallo stesso punto (infatti a distanze molto piccole entrano in gioco forze nucleari che sono attrattive e non repulsive) assumiamo che il grafico sia in funzione del tempo, con il tempo che parte dall’istante t=0.
Indichiamo con q il valore della carica di ciascuna massa, r la distanza tra esse ed \({{r}_{0}}\) la distanza iniziale tra le due cariche.
Possiamo scrivere l’espressione del potenziale del campo elettrico generato dalla carica ferma in funzione della distanza:
\(V\left( r \right)={{k}_{0}}\frac{q}{r}\)
Assumendo che la seconda carica parte da ferma, l’energia cinetica è pari alla variazione di energia potenziale:
\(\frac{1}{2}m{{v}^{2}}={{k}_{0}}{{q}^{2}}\frac{1}{{{r}_{0}}}-{{k}_{0}}{{q}^{2}}\frac{1}{r}={{k}_{0}}{{q}^{2}}\left( \frac{1}{{{r}_{0}}}-\frac{1}{r} \right)\)
E quindi la velocità è legata alla distanza tra le due cariche dalla relazione:
\(v=\sqrt{\frac{2{{k}_{0}}{{q}^{2}}}{m}\left( \frac{1}{{{r}_{0}}}-\frac{1}{r} \right)}\)
La velocità raggiunge una velocità limite nello spazio e naturalmente questo vale anche nel tempo.
\(\underset{r\to \infty }{\mathop{\lim }}\,v=q\sqrt{\frac{2{{k}_{0}}}{m{{r}_{0}}}}\)
E visto che la distanza aumenta aumenta in funzione del tempo, si ha che \(r\to \infty \) \(\Rightarrow \) \(t\to \infty \) e quindi:
\(\underset{t\to \infty }{\mathop{\lim }}\,v=q\sqrt{\frac{2{{k}_{0}}}{m{{r}_{0}}}}\)
Naturalmente questo risultato esprime qualcosa che poteva essere previsto anche senza fare calcoli. Infatti aumentando la distanza tra le due cariche, in accordo con la legge di Coulomb, secondo la quale la forza è inversamente proporzionale al quadrato della distanza, si avrà che a distanza abbastanza grande, la forza di interazione tra le cariche diventa trascurabile, e il moto in assenza di forze è rettilineo uniforme.
La risposta alla domanda è NO, perché si prevede che la velocità deve tendere ad un asintoto orizzontale.
Inoltre l’incremento di velocità in due intervalli successivi di tempo dovrebbe essere sempre più piccolo, visto che la forza e di conseguenza l’accelerazione tendono a diminuire in funzione del tempo. Il grafico corretto della velocità al variare del tempo dovrebbe essere una funzione concava e non convessa.
Soluzione quesito 8 – Soluzione Simulazione Seconda Prova di Matematica e Fisica
a) Possiamo usare le leggi della trigonometria per riscrivere la legge oraria di x(t) come quella di un moto armonico.
Dalle formula trigonometrica di linearità si ha che \({{sin }^{2}}x=\frac{1}{2}-\frac{1}{2}cos \left( 2x \right)\).
Applicando la formula ad x(t) possiamo riscrivere la legge oraria nel seguente modo:
\(x(t)=\frac{a}{2}-\frac{a}{2}cos \left( 6t-\frac{pi }{2} \right)=\frac{a}{2}-\frac{a}{2}sin \left( 6t \right)\)
A questo punto è subito chiaro che x(t) descrive il moto di un corpo che oscilla rispetto alla posizione di riposo posta in x=a/2, ha un ampiezza di oscillazione pari ad a/2, una pulsazione (omega =6) e periodo \(T=\frac{2\pi }{\omega }=\frac{\pi }{3}\)
b) L’istante in cui il punto raggiunge per la prima volta la massima distanza dalla origine coincide con l’istante temporale in cui il seno assume per la volta il valore -1 che coincide con l’istante in cui l’argomento del seno assume valore \(\frac{3}{2}\pi \) .
\(6t=\frac{3}{2}\pi \Rightarrow t=\frac{\pi }{4}\)
