Teorema di unicità dell’estremo superiore dimostrazione

Il Teorema di unicità dell’estremo superiore è un concetto matematico importante che riguarda gli insiemi reali che sono superiormente limitati. Questo teorema afferma che per ogni insieme di numeri reali che ha un limite superiore, esiste un unico estremo superiore.

Nel video che segue, vedrete una dimostrazione di questo teorema in azione. La dimostrazione si concentra sui concetti fondamentali che stanno dietro a questo teorema, spiegando in dettaglio i punti chiave in modo chiaro e comprensibile. Vedrete come gli insiemi di numeri reali superiormente limitati sono ordinati e come questo ordine influisce sull’estremo superiore.

Questa dimostrazione vi aiuterà a comprendere meglio come funzionano i concetti matematici alla base del Teorema di unicità dell’estremo superiore. Potrete vedere come ogni passaggio della dimostrazione porta logicamente alla conclusione che c’è un solo estremo superiore per gli insiemi reali superiormente limitati. Seguire questa dimostrazione vi darà una visione chiara e dettagliata di questo importante teorema matematico.

Spero che questo video possa esservi utile per approfondire i concetti fondamentali della dimostrazione del Teorema di unicità dell’estremo superiore.

In seguito riporto una dimostrazione scritta, del teorema, ma se non l’hai già fatto ti consiglio di guardare il video, perché troverai delle spiegazioni più chiare che mettono in evidenza i punti chiave della dimostrazione del Teorema di unicità dell’estremo superiore.

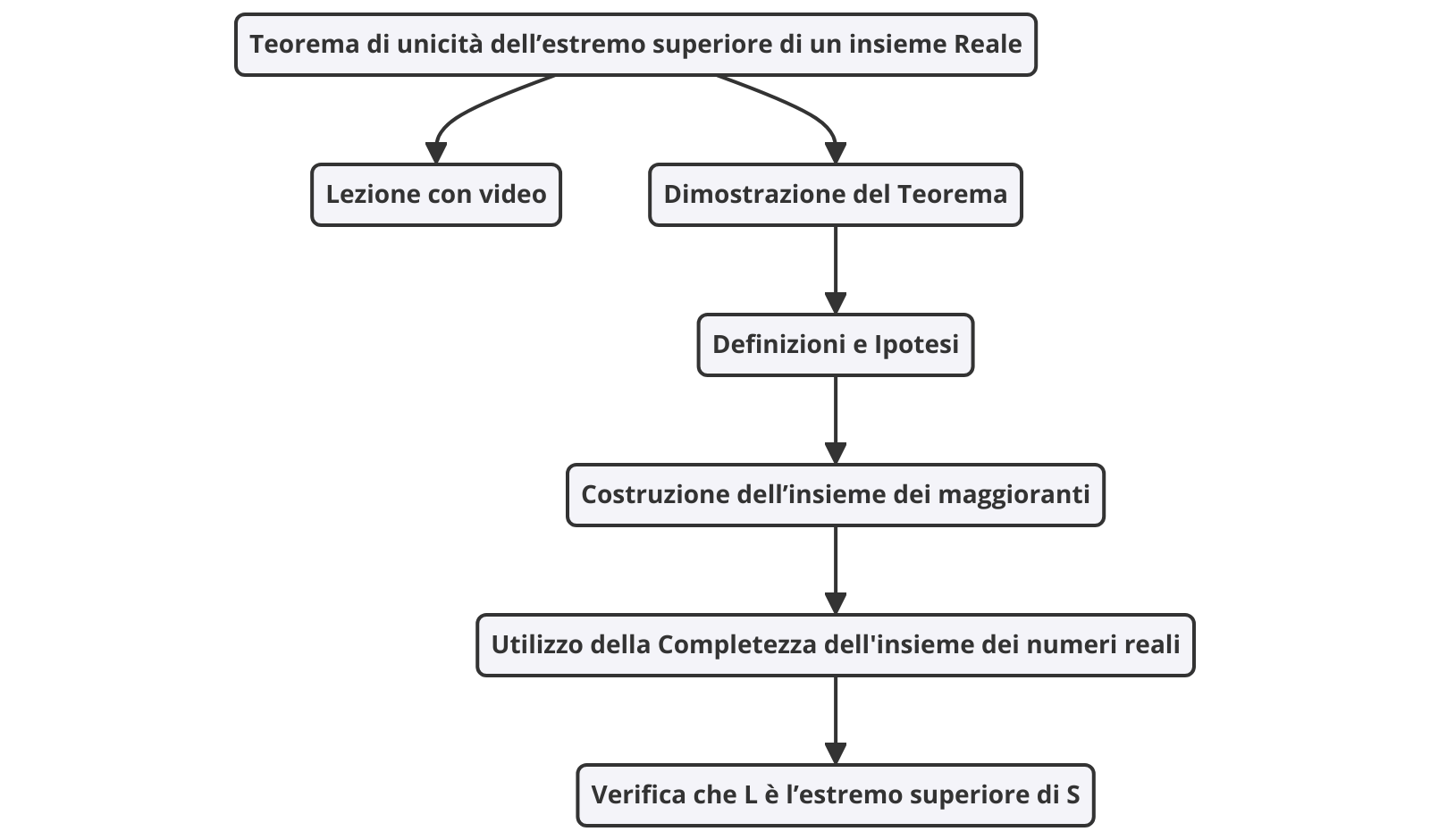
Dimostrazione del Teorema di unicità dell’estremo superiore dimostrazione

Definizioni e Ipotesi

Insieme $ S $: Si consideri $ S $ un insieme non vuoto di numeri reali.

Limitato Superiormente: Si supponga che $ S $ sia limitato superiormente. Ciò significa che esiste almeno un numero reale $ M $ tale che $ s \leq M $ per ogni $ s \in S $.

Costruzione dell’insieme dei maggioranti

Insieme $ B $: Definiamo $ B $ come l’insieme di tutti i maggioranti di $ S $. Formalmente:

$ B = \{ b \in \mathbb{R} : s \leq b \text{ per ogni } s \in S \} $

Proprietà di $ B $: Per ipotesi, $ B $ non è vuoto perché contiene il maggiorante $ M $. Inoltre, $ B $ è evidentemente limitato inferiormente da ogni elemento di $ S $ (dato che ogni $ s $ in $ S $ è inferiore a ogni $ b $ in $ B $).

Utilizzo della Completezza di $ \mathbb{R} $

Estremo inferiore di $ B $: Dal fatto che $ \mathbb{R} $ è un insieme completo, sappiamo che ogni insieme non vuoto limitato inferiormente in $ \mathbb{R} $ ha un estremo inferiore in $ \mathbb{R} $. Pertanto, possiamo definire $ L = \inf B $, che esiste per la completezza di $ \mathbb{R} $.

Verifica che $ L $ è l’estremo superiore di $ S $

$ L $ è un maggiorante: Per definizione di estremo inferiore, per ogni $ \epsilon > 0 $, esiste un $ b \in B $ tale che $ L \leq b < L + \epsilon $. Poiché $ b $ è un maggiorante di $ S $, segue che $ s \leq b < L + \epsilon $ per ogni $ s \in S $. Di conseguenza, $ s \leq L $ per ogni $ s \in S $, mostrando che $ L $ è un maggiorante di $ S $.

$ L $ è il minimo maggiorante: Supponiamo per assurdo che esista un $ L’ < L $ che sia anche un maggiorante di $ S $. Allora $ L’ $ sarebbe un elemento di $ B $ (perché è un maggiorante di $ S $), il che contraddice la definizione di $ L $ come il più piccolo elemento di $ B $ (estremo inferiore). Questa contraddizione mostra che non può esistere un maggiorante di $ S $ che sia minore di $ L $.

Conclusione

Pertanto, $ L = \inf B $ rappresenta l’estremo superiore di $ S $. Questo dimostra che ogni insieme non vuoto di numeri reali, limitato superiormente, ha un estremo superiore in $ \mathbb{R} $. Questo risultato è di fondamentale importanza in diverse aree dell’analisi matematica, assicurando la coerenza e la completezza dell’insieme dei numeri reali rispetto alle operazioni limite.

Un’estensione di questa dimostrazione si trova nel concetto di estremo inferiore, che rappresenta il più piccolo dei maggioranti di un insieme ed è l’opposto dell’estremo superiore. Insieme all’estremo superiore, l’estremo inferiore gioca un ruolo cruciale nella caratterizzazione della completezza degli insiemi di numeri reali.

Inoltre, l’utilizzo degli estremi superiori e inferiori è comune nella teoria delle successioni e delle serie, dove è essenziale per determinare la convergenza e la divergenza delle sequenze numeriche. Questo concetto fornisce una base solida per lo studio delle proprietà dei numeri reali e la loro rappresentazione geometrica su una retta reale.

In conclusione, la dimostrazione dell’esistenza degli estremi superiori per insiemi limitati superiormente è di fondamentale importanza nell’analisi matematica. Contribuisce alla comprensione della struttura e delle proprietà dei numeri reali e fornisce una base solida per lo sviluppo di concetti più avanzati all’interno di questa disciplina.