2. Esercizio svolto – Integrale triplo su cilindro tagliato da due piani
$\iiint\limits_{A}{{{( y+z )}^{2}}dxdydz} $,
$A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,\,{{y}^{2}}+{{z}^{2}}\le 25,\,\,\,\,z\le x+4,\,\,x\le 1\}$
Continua a leggere l’esercizio svolto – Integrale triplo su cilindro tagliato da due piani.

Per prima cosa proviamo a capire di cosa si tratta l’insieme di integrazione.
${{y}^{2}}+{{z}^{2}}=25$ rappresenta l’equazione di un cilindro avente coassiale all’asse x e il minore o uguale sta ad indicare che bisogna prendere la parte interna.
Le equazioni $x=z$ e $x=1$ sono due piani che contengono l’asse y. L’insieme A è costituito dalla parte cilindro compresa tra i due piani.
Considerato che ${{y}^{2}}+{{z}^{2}}\le 25$ allora si ha che $-5\le z\le 5$ e inoltre aggiungendo le altre due condizioni $\{ z\le x+4,\,\,x\le 1 \}$ si ha che $-5\le z\le 5$, $z-4\le x\le 1$.
Possiamo scrivere l’integrale triplo con i suoi estremi di integrazione:
$\int\limits_{z=-5}^{5} \int\limits_{x=z-4}^{1} \int\limits_{y=-\sqrt{25-z^2}}^{\sqrt{25-z^2}} (y+z)^2 \,dxdydz =$
$\frac{1}{3} \cdot \int\limits_{z=-5}^{5} ( (z+\sqrt{25-z^2})^3 – (z-\sqrt{25-z^2})^3 ) dz \cdot \int\limits_{x=z-4}^{1} dx$
L’integrale più esterno è immediato ed è dato dalla differenza degli estremi.
$\int\limits_{x=z-4}^{1}{dx}=1-(z-4)=5-z$
A questo punto otteniamo un integrale nella sola variabile z
$\frac{1}{3}\int\limits_{z=-5}^{5}(5-z) \cdot [ {{(z+\sqrt{25-{{z}^{2}}})}^{3}} – {{(z-\sqrt{25-{{z}^{2}}})}^{3}} ]dz$
Svolgendo i conti e facendo tutti i passaggi algebrici possiamo riscrivere l’integrale nella forma
$\int\limits_{z=-5}^{5} \frac{2}{3}( -2{{z}^{3}}+10{{z}^{2}}-25z+125 )\sqrt{25-{{z}^{2}}}dz$
A questo punto osserviamo che l’intervallo di integrazione è simmetrico e quindi le funzioni dispari hanno integrale nullo, ovvero
$\int\limits_{z=-5}^{5} z^3 \sqrt{25-z^2} \,dz = \int\limits_{z=-5}^{5} z \sqrt{25-z^2} \,dz = 0$
E quindi l’integrale diventa:
$\int\limits_{z=-5}^{5}{\frac{2}{3}( 10{{z}^{2}}+125 )\sqrt{25-{{z}^{2}}}dz\,}=$ $\frac{20}{3}\int\limits_{z=-5}^{5}{{{z}^{2}}\sqrt{25-{{z}^{2}}}dz\,}+\frac{250}{3}\int\limits_{z=-5}^{5}{\sqrt{25-{{z}^{2}}}dz\,}$
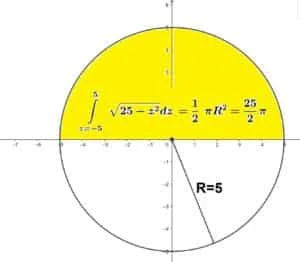
A questo punto andiamo a risolvere singolarmente i due integrali. Cominciamo dal secondo, possiamo risolverlo facendo una semplice osservazione geometrica, come mostrato in figura, l’integrale $\int\limits_{z=-5}^{5}{\sqrt{25-{{z}^{2}}}dz\,}$ rappresenta l’area di una semicirconferenza di raggio R=5, pertanto la suo valore è $\int\limits_{z=-5}^{5}{\sqrt{25-{{z}^{2}}}dz\,}=\frac{25}{2}\pi $
Per concludere andiamo a risolvere $\int\limits_{z=-5}^{5}{{{z}^{2}}\sqrt{25-{{z}^{2}}}dz\,}$ e possiamo farlo attraverso la sostituzione
$\int\limits_{z=-\frac{\pi}{2}}^{\frac{\pi}{2}} 25\sin^2(x) \sqrt{25 – 25\sin^2(x)} \cdot 5\cos(x) \,dx =$
$\int\limits_{z=-\frac{\pi}{2}}^{\frac{\pi}{2}} 625\sin^2(x) \cos^2(x) \,dx =$
$\frac{625}{4} \int\limits_{z=-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin^2(2x) \,dx =$
$\frac{625}{8} \pi$
Possiamo concludere che il risultato dell’integrale triplo è:
$\frac{20}{3} \int\limits_{z=-5}^{5} z^2 \sqrt{25-z^2} \,dz + \frac{250}{3} \int\limits_{z=-5}^{5} \sqrt{25-z^2} \,dz =$
$\frac{20}{3} \cdot \frac{625}{8}\pi + \frac{250}{3} \cdot \frac{25}{2}\pi = \frac{3125}{2}\pi$
