3. Integrale triplo svolto su volume compreso tra due sfere decentrate
$\iiint\limits_{A}{( x+{{z}^{3}}\sin {{y}^{2}} )dxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,\,2x\le {{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 1,\,x\ge 0 \}$
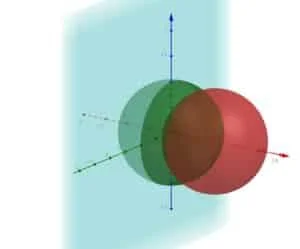
Per prima cosa proviamo a capire di cosa si tratta l’insieme di integrazione.
Si tratta del volume compreso tra due sfere decentrate e un piano. Vediamo singolarmente le superfici che fanno da contorno al volume rappresentato dall’insieme A.
La prima superficie è una sfera decentrata rispetto all’origine e per ottenere centro e raggio completiamo i quadrati:
${{x}^{2}}+{{y}^{2}}+{{z}^{2}}=2x$
${{x}^{2}}-2x+{{y}^{2}}+{{z}^{2}}=0$
${{x}^{2}}-2x+1+{{y}^{2}}+{{z}^{2}}=+1$
${{( x-1 )}^{2}}+{{y}^{2}}+{{z}^{2}}=+1$
Si tratta quindi di una sfera centrata in (1,0,0) e di raggio R=1.
La seconda sfera di equazione ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}=1$ è centrata nell’origine e ha raggio unitario.
Per concludere x=0 è un piano e vediamo il grafico tridimensionale dell’insieme da diversi punti di vista.
Passiamo in coordinate cilindriche per descrivere meglio l’insieme di integrazione:
$\begin{cases}x = x \\y = \rho \cos \theta \\z = \rho \sin \theta\end{cases}$
dove $\rho \ge 0$ ,$\theta \in [ 0,2\pi ]$ , $|\det J|=\rho $
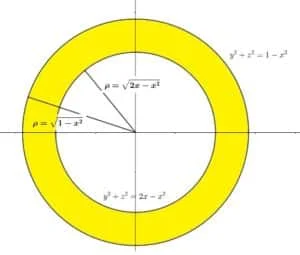
Si osserva che fissando x, si ha che la sezione del solido è la parte di piano compresa tra due cerchi $2x-{{x}^{2}}\le {{y}^{2}}+{{z}^{2}}\le 1-{{x}^{2}}$, come in figura.
Riscriviamo a questo punto le disequazioni che descrivono l’insieme A, facendo la sostituzione delle coordinate polari.
$2x\le {{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 1$
$2x-{{x}^{2}}\le {{\rho }^{2}}\le 1-{{x}^{2}}$
$\sqrt{2x-{{x}^{2}}}\le \rho \le \sqrt{1-{{x}^{2}}}$
Ed inoltre bisogna imporre $2x-{{x}^{2}}\le 1-{{x}^{2}}$ per capire tra quali valori varia la variabile x, e si ha $2x-1\le 0$ , quindi $x\le \frac{1}{2}$. Aggiungendo l’altra condizione contenuta in A, e cioè $x\ge 0$, si ha che $0\le x\le \frac{1}{2}$.
Non si hanno condizioni che limitano la variabile θ, che quindi varia nell’intero intervallo [0,2π].
In coordinate polari l’insieme A diventa:
${A}’=\{ ( \rho ,\theta ,\phi )\in {{\mathbb{R}}^{3}}:\,\,0\le x\le \frac{1}{2},\,\,0\le \theta \le 2\pi ,\,\,\sqrt{2x-{{x}^{2}}}\le \rho \le \sqrt{1-{{x}^{2}}}\, \}$
A questo punto spezziamo l’integrale triplo nella somma di due integrali $\iiint\limits_{A}{( x+{{z}^{3}}\sin {{y}^{2}} )dxdydz}=$ $\iiint\limits_{A}{xdxdydz}+\iiint\limits_{A}{{{z}^{3}}\sin {{y}^{2}}dxdydz}=$ $\iiint\limits_{A}{xdxdydz}$
Il secondo integrale fa zero per motivi di simmetria $\iiint\limits_{A}{{{z}^{3}}\sin {{y}^{2}}dxdydz}=0$
A questo punto riscriviamo l’integrale in coordinate polari ricordando di moltiplicare per il modulo del determinante della matrice Jacobiana.
$\iiint\limits_{A}{xdxdydz}=$ $\iiint\limits_{{{A}’}}{x\rho d\rho d\theta dz}$
A questo punto scriviamo gli estremi e procediamo al calcolo dell’integrale:
$\int\limits_{x=0}^{1/2}{x\int\limits_{\theta =0}^{2\pi }{\int\limits_{\rho=\sqrt{2x-{{x}^{2}}}}^{\sqrt{1-{{x}^{2}}}}{\rho }}}\cdot d\rho d\theta d\phi =$ $\int\limits_{0}^{2\pi }{d\theta }\cdot \int\limits_{x=0}^{1/2}{x[ \frac{{{\rho }^{2}}}{2} ]_{\sqrt{2x-{{x}^{2}}}}^{\sqrt{1-{{x}^{2}}}}}dx=$ $[ \theta ]_{0}^{2\pi }\int\limits_{x=0}^{1/2}{x\frac{1-2x}{2}}dx=$ $2\pi \int\limits_{x=0}^{1/2}{x\frac{1-2x}{2}}dx=$
$\pi \int\limits_{x=0}^{1/2}{x-2{{x}^{2}}}dx=$ $\pi [ \frac{1}{2}{{x}^{2}}-\frac{2}{3}{{x}^{3}} ]_{0}^{1/2}=\frac{\pi }{24}$.
Possiamo finalmente concludere che il risultato dell’integrale triplo è $\iiint\limits_{A}{( x+{{z}^{3}}\sin {{y}^{2}} )dxdydz}=\frac{\pi }{24}$:
