6. Integrale triplo su un insieme che in coordinate cartesiane è un quarto di cilindro
$\iiint\limits_{A}{xzdxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,\,,{{x}^{2}}+{{y}^{2}}\le 1,\,\,x\ge 0,y\ge 0\,\,,-1\le z\le 0\, \}$
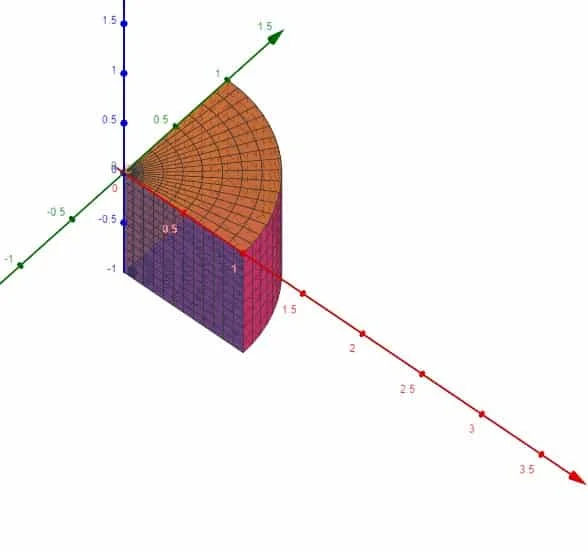
L’insieme di integrazione è costituito da un cilindro tagliato da quattro piani. Come si vede nell’immagine si tratta di uno spicco di cilindro di altezza unitaria e con un’apertura pari a π/2, ovvero esattamente pari ad un quarto di cilindro.
Questo insieme sembra pensato a posta per essere descritto in coordinate cilindriche e infatti faremo esattamente così.
Per cominciare riportiamo il cambio di coordinate che permette di passare dalle coordinate cartesiane a quelle cilindriche.
$\begin{cases} x=\rho \cos \theta \\ y=\rho \sin \theta \\ z=z \\\end{cases} $
dove $\rho \ge 0$ ,$0\le \theta \le 2\pi $ , $|\det J|=\rho $
Cambio di coordinate nell’insieme di integrazione
A questo punto facciamo il cambio di coordinate sull’insieme di integrazione, modificando una alla volta le espressioni che lo caratterizzano. Partiamo dalla disequazione che descrive il cilindro:
${{x}^{2}}+{{y}^{2}}\le 1$
${{\rho }^{2}}\le 1$
$0\le \rho \le 1$
La condizione $\{ x\ge 0,y\ge 0 \}$ equivale a dire la parte di spazio definita dal primo quadrante del piano cartesiano $(x,y)$. In coordinate cilindriche questo si traduce limitando l’angolo θ nell’intervallo tra 0 e π/2.
$\{ x\ge 0,y\ge 0 \}$ $\rightarrow $ $0\le \theta \le \frac{\pi }{2}$
In coordinate cilindriche l’insieme diventa
${A}’=\{ ( \rho ,\theta ,z )\in {{\mathbb{R}}^{3}}:\,\,-1\le z\le 0,\,\,0\le \theta \le \frac{\pi }{2},\,\,0\le \rho \le 1\, \}$
Si tratta di un insieme normale rispetto a tutte le variabili, perché ognuna varia all’interno di un certo intervallo e sono tutte indipendenti tra loro.
Cambio di coordinate nell’integrale
A questo punto facciamo il cambio di coordinate nell’integrale ricordandoci di moltiplicare per il valore assoluto del determinante della matrice Jacobiana.
$\iiint\limits_{A}{xzdxdydz}=$ $\iiint\limits_{{{A}’}}{\rho \cos \theta \cdot z\,\rho d\rho d\theta dz}=$ $\int\limits_{0}^{1}{\int\limits_{0}^{\pi /2}{\int\limits_{-1}^{0}{\cos \theta d\theta z{{\rho }^{2}}d\rho dz}=}}$
Si tratta di un integrale a variabili separabili, che può essere riscritto come il prodotto tra tre integrali indipendenti ciascuno nella propria variabile.
$\int\limits_{0}^{1}{{{\rho }^{2}}d\rho }\cdot \int\limits_{0}^{\pi /2}{\cos \theta d\theta }\cdot \int\limits_{-1}^{0}{zdz}=$
Calcoliamo i singoli integrali per poi moltiplicarli tra loro.
$\int\limits_{0}^{1}{{{\rho }^{2}}d\rho }=\frac{1}{3}[ {{\rho }^{3}} ]_{0}^{1}=\frac{1}{3}$
$\int\limits_{0}^{\pi /2}{\cos \theta d\theta }=[ \sin \theta ]_{0}^{\pi /2}=1$
$\int\limits_{-1}^{0}{zdz}=\frac{1}{2}[ {{z}^{2}} ]_{-1}^{0}=-\frac{1}{2}$
Possiamo a questo punto tornare all’integrale principale e darne il risultato.
$\int\limits_{0}^{1}{{{\rho }^{2}}d\rho }\cdot \int\limits_{0}^{\pi /2}{\cos \theta d\theta }\cdot \int\limits_{-1}^{0}{zdz}=$ $\frac{1}{3}\cdot 1\cdot ( -\frac{1}{2} )=$ $-\frac{1}{6}$
Il risultato dell’integrale è $\iiint\limits_{A}{xzdxdydz}=-\frac{1}{6}$.
