7. Esempio di integrale triplo svolto in coordinate sferiche
$\iiint\limits_{A}{\frac{1}{{{z}^{3}}}dxdydz}$ ,
$A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,z\ge \sqrt{3{{x}^{2}}+3{{y}^{2}}},\,\frac{1}{4}\le {{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 1\, \}$
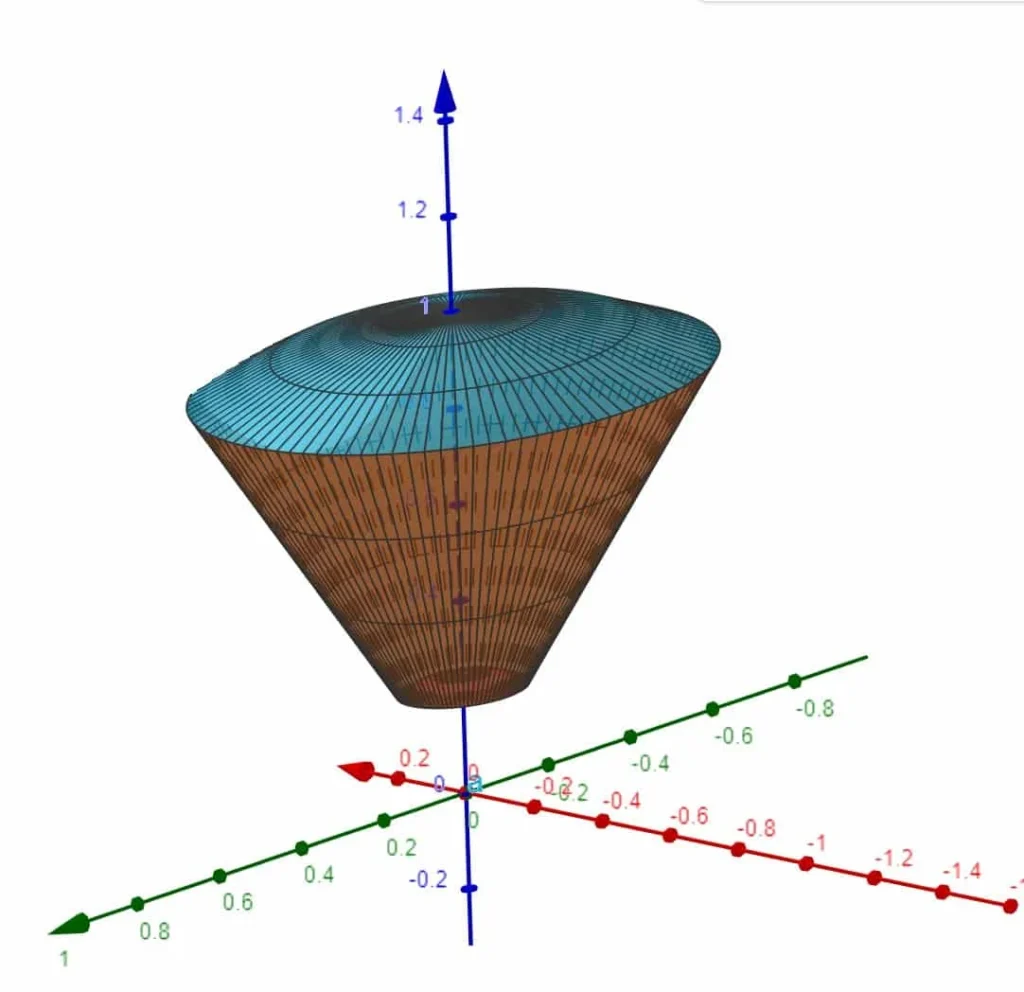
L’insieme A descrive il solido compreso tra la superficie di due sfere concentriche di centro nell’origine degli assi e un cono.
Come già detto nell’introduzione si tratta di un integrale che risulta particolarmente agevole in coordinate sferiche.
Passaggio in coordinate sferiche nell’insieme di integrazione:
Riportiamo come prima cosa il sistema di equazione che permette il passaggio da coordinate cartesiane a sferiche.
$ \begin{cases} x = \rho \cos \theta \sin \phi \\ y = \rho \sin \theta \sin \phi \\ z = \rho \cos \phi \end{cases} $
Dove:
– $\rho$ rappresenta la distanza radiale del punto dall’origine,
– $\theta$ è l’angolo azimutale misurato dal semiasse positivo $x$ nel piano $xy$,
– $\phi$ è l’angolo zenitale misurato dal semiasse positivo $z$.
Ricordiamo inoltre che $\rho \ge 0$ , $0\le \theta \le 2\pi $ , $0\le \phi \le \pi $ , $|\det J|={{\rho }^{2}}\sin \phi $
E che sono utili da ricordare anche le seguenti relazioni facilmente ricavabili dal sistema di cambio di coordinate sferiche: $\sin \phi \ge 0$ ,${{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{\rho }^{2}}$ , ${{x}^{2}}+{{y}^{2}}={{\rho }^{2}}{{\sin }^{2}}\phi $
A questo punto riscriviamo ciascuna espressione nel sistema di coordinate sferiche. Partiamo dall’equazione del cono.
$z\ge \sqrt{3{{x}^{2}}+3{{y}^{2}}}$
$\rho \cos \phi \ge \sqrt{3}\rho \sin \phi $ $\rightarrow $ $\tan \phi \le \frac{1}{\sqrt{3}}$
$0\le \phi \le \frac{\pi }{6}$
Passiamo ora all’intersezione tra le due sfere.
$\frac{1}{4}\le {{x}^{2}}+{{y}^{2}}+{{z}^{2}}\le 1$
$\frac{1}{4}\le {{\rho }^{2}}\le 1$
$\frac{1}{2}\le \rho \le 1$
Per quanto riguarda la variabile θ non ci sono limitazioni imposte dalle condizioni in A, quindi si ha che $0\le \theta \le 2\pi $.
L’insieme nel nuovo sistema di coordinate diventa:
${A}’=\{0\le \phi \le \frac{\pi }{6}, \frac{1}{2}\le \rho \le 1,0\le \theta \le 2\pi \, \}$
Passaggio in coordinate sferiche nell’integrale:
Notiamo che l’insieme è normale rispetto a tutte le variabili.
Passiamo al cambio di coordinate all’interno dell’integrale ricordandoci di moltiplicare per il modulo del determinante della matrice Jacobiana.
$\iiint\limits_{A}{\frac{1}{{{z}^{3}}}dxdydz}=$ $\iiint\limits_{{{A}’}}{\frac{1}{{{\rho }^{3}}{{\cos }^{3}}\phi }{{\rho }^{2}}\sin \phi d\rho d\theta d\phi }=$ $\int\limits_{0}^{2\pi }{\int\limits_{0}^{\pi /6}{\int\limits_{1/2}^{1}{\frac{1}{\rho }}\frac{\sin \phi }{{{\cos }^{3}}\phi }d\phi }\cdot d\theta }\cdot d\rho =$
Si tratta di un integrale a variabili separabili che può essere riscritto come il prodotto di tre integrali indipendenti:
$=\int\limits_{0}^{2\pi }{d\theta }\cdot \int\limits_{0}^{\pi /6}{\frac{\sin \phi }{{{\cos }^{3}}\phi }d\phi }\cdot \int\limits_{1/2}^{1}{\frac{1}{\rho }d\rho }$
A questo punto calcoliamo singolarmente ciascuno degli integrali:
$\int\limits_{0}^{2\pi }{d\theta }=2\pi $
$\int\limits_{0}^{\pi /6}{{{\cos }^{-3}}\phi \sin \phi d\phi }=$ $\frac{1}{2}[ {{\cos }^{-2}}\phi ]_{0}^{\pi /6}=\frac{1}{6}$
$\int\limits_{1/2}^{1}{\frac{1}{\rho }d\rho }=\log 2$
Andiamo a sostituire nell’integrale principale.
$\int\limits_{0}^{2\pi }{d\theta }\cdot \int\limits_{0}^{\pi /6}{\frac{\sin \phi }{{{\cos }^{3}}\phi }d\phi }\cdot \int\limits_{1/2}^{1}{\frac{1}{\rho }d\rho }=$ $2\pi \cdot \frac{1}{6}\cdot \log 2=$ $\frac{\pi \log 2}{3}$
Possiamo concludere che il risultato dell’integrale è $\iiint\limits_{A}{\frac{1}{{{z}^{3}}}dxdydz}=\frac{\pi \log 2}{3}$.
Approfondimento
Esercizio molto utile per comprendere meglio la parametrizzazione delle superfici: provare a descrivere la superficie laterale dell’insieme A attraverso una opportuna parametrizzazione.
Riportiamo una possibile soluzione:
${{\Sigma }_{1}}=( \frac{1}{4}\cos \theta \sin \phi ,\frac{1}{4}\sin \theta \sin \phi ,\frac{1}{4}\cos \phi ),0\le \theta \le 2\pi ,0\le \phi \le \frac{\pi }{6}$
${{\Sigma }_{2}}=( \cos \theta \sin \phi ,\sin \theta \sin \phi ,\cos \phi ),0\le \theta \le 2\pi ,0\le \phi \le \frac{\pi }{6}$
${{\Sigma }_{3}}=( \rho \cos \theta ,\rho \sin \theta ,\sqrt{3}\rho ),0\le \theta \le 2\pi ,\frac{1}{8}\le \rho \le \frac{1}{2}$
