8. Soluzione di integrale triplo con valore assoluto
$\iiint\limits_{A}{|x|dxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,{{y}^{2}}+{{z}^{2}}\le 1,z\ge {{x}^{2}}\, \}$
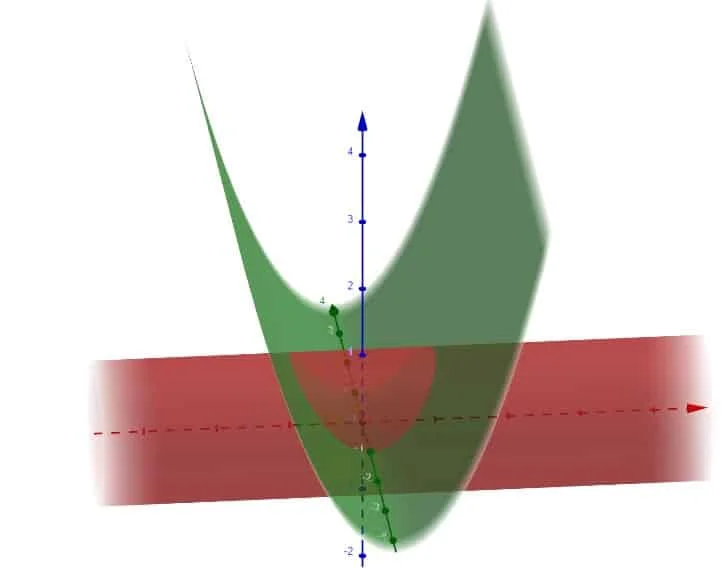
In figura si riporta il grafico dell’insieme A su cui dobbiamo integrare. Si tratta di un cilindro tagliato da una superficie parabolica.
Per questo tipo di integrale non facciamo alcun cambio di coordinate ma ci limitiamo a riscrivere meglio l’insieme in coordinate cartesiane.
La funzione integranda $|x|$ è una funzione pari e data la simmetria dell’insieme di integrazione, ci permette di integrare solo su metà insieme ${{A}_{1}}$ e moltiplicare il risultato per due.
$\iiint\limits_{A}{|x|dxdydz}=2\iiint\limits_{{{A}_{1}}}{xdxdydz}$, ${{A}_{1}}=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,{{y}^{2}}+{{z}^{2}}\le 1,z\ge {{x}^{2}},x\ge 0\, \}$
Partiamo dalla prima espressione:
${{y}^{2}}+{{z}^{2}}\le 1$
${{z}^{2}}\le 1-{{y}^{2}}$
$z\le \sqrt{1-{{y}^{2}}}$
Per motivi di dominio (radice quadrata) si ha che:
$-1\le y\le 1$
Lo scopo finale è ottenere un insieme dove la prima variabile varia tra due numeri, la seconda variabile tra due funzioni che dipendono al più dalla variabile precedente e una terza variabile compresa tra due funzioni che dipendono dalle altre variabili.
${{x}^{2}}\le z\le \sqrt{1-{{y}^{2}}}$
$0\le x\le 1$
${{x}^{2}}\le \sqrt{1-{{y}^{2}}}$
$x\le \sqrt[4]{1-{{y}^{2}}}$
Per concludere otteniamo l’insieme riscritto in questa forma:
${{A}_{1}}=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,-1\le y\le 1,\,0\le x\le \sqrt[4]{1-{{y}^{2}}},\,{{x}^{2}}\le z\le \sqrt{1-{{y}^{2}}} \}$
A questo punto torniamo all’integrale e risolviamolo. Si riportano di seguito i vari passaggi.
$\iiint\limits_{{{A}_{1}}} xdxdydz = \int\limits_{y=-1}^{1} \int\limits_{x=0}^{\sqrt[4]{1-y^{2}}} x \int\limits_{z=x^{2}}^{\sqrt{1-y^{2}}} dz \,dxdy$
$= \int\limits_{y=-1}^{1} \int\limits_{x=0}^{\sqrt[4]{1-y^{2}}} x \left( \sqrt{1-y^{2}} – x^{2} \right) \,dxdy$
$= \int\limits_{y=-1}^{1} \sqrt{1-y^{2}} \int\limits_{x=0}^{\sqrt[4]{1-y^{2}}} x dxdy \,- $ $\int\limits_{y=-1}^{1} \int\limits_{x=0}^{\sqrt[4]{1-y^{2}}} x^{3} \,dxdy$
$= \int\limits_{y=-1}^{1} \frac{1-y^{2}}{2} dy \, – \int\limits_{y=-1}^{1} \frac{1-y^{2}}{4} dy$
$= \frac{1}{4} \int\limits_{y=-1}^{1} 1-y^{2} \,dy = \frac{1}{4} \left[ y – \frac{y^{3}}{3} \right]_{-1}^{1} = \frac{1}{3}$
A questo punto ritorniamo all’integrale principale:
$\iiint\limits_{A}{|x|dxdydz}=2\iiint\limits_{{{A}_{1}}}{xdxdydz}=\frac{2}{3}$
Possiamo dare il risultato dell’integrale che è $\frac{2}{3}$.
