Indice dei contenuti
Questa pagina è dedicata a fornirti delle metodologie per lo svolgimento di Esercizi su massimi e minimi in 2 variabili. Quindi mettiti comodo e segui i passaggi con attenzione perché possono esserti molto utili per il tuo esame di analisi matematica. Questi esercizi sono svolti con cura e attenzione ai dettagli, ma anche con un pizzico di originalità mostrando quelli che sono i principali metodi per approcciare a questo tipo di problema.
Esercizi su massimi e minimi in 2 variabili su insiemi compatti (METODO DELLE CURVE DI LIVELLO)
Per cominciare propongo un metodo un pò inusuale, ma molto intuitivo ed elegante, che è quello del metodo delle curve di livello per risolvere Esercizi su massimi e minimi in 2 variabili. Il metodo consiste nel capire in che direzione crescono le curve di livello del grafico e in quali punti intercettano l’insieme compatto su cui stiamo cercando massimi e minimi.
ESERCIZIO 1
Cercare massimo e minimo assoluto di$f\left( x,y \right)={{x}^{2}}+{{y}^{2}}-4x$ sull’insieme $A=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}:\,\,1\le y\le {{e}^{x}},\,\,\,x\le 3 \right\}$ .
Le curve di livello della funzione $f\left( x,y \right)$sono circonferenze ${{x}^{2}}+{{y}^{2}}-4x=k$
${{x}^{2}}-4x+4+{{y}^{2}}=k+4$, ${{\left( x-2 \right)}^{2}}+{{y}^{2}}={{\left( \sqrt{k+4} \right)}^{2}}$, sono circonferenze di centro $C=\left( 2,0 \right)$ e raggio $R=\sqrt{4+k}$ .
All’aumentare di $k$ aumenta anche il raggio della circonferenza. Pertanto bisogna individuare il punto a minima distanza da $C$ ovvero ${{P}_{0}}$ e il punto a massima distanza cioè ${{P}_{1}}$.
In ${{P}_{0}}$ la circonferenza è tangente alla retta di equazione $y=1$ .
${{x}^{2}}+{{1}^{2}}-4x=k\,\,\,\Rightarrow \,\,\,{{x}^{2}}-4x+1-k\,\,=0$ . La circonferenza è tangente alla retta se $\Delta =0\,\,\,\Rightarrow \,\,\,16-4+4k=0\,\,\,\Rightarrow \,\,\,k=-3$ . Pertanto $\underset{x\in A}{\mathop{\min }}\,f=-3$
Il punto a massima distanza è in ${{P}_{1}}=\left( 3,{{e}^{3}} \right)$ , punto di intersezione tra la retta e l’esponenziale.
$\underset{x\in A}{\mathop{\max }}\,f=f\left( {{P}_{1}} \right)=9+{{e}^{6}}-12={{e}^{6}}-3$
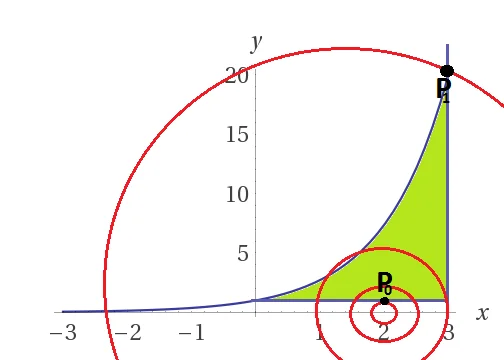
Nella figura quelle che vediamo colorate in rosso sono le curve di livello, mentre in verde c’è l’insieme del piano su cui andiamo a cercare massimi e minimi.
massimi e minimi su compatti – metodo delle curve di livello
ESERCIZIO 2
$f\left( x,y \right)=\frac{x-y+1}{x+3}$ su $A=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}:\,\,2-\frac{2}{3}{{x}^{2}}\le y\le 3-{{x}^{2}} \right\}$
L’insieme A è rappresentato geometricamente dallo spazio compreso tra due parabole. I punti di intersezioni tra esse sono $2-\frac{2}{3}{{x}^{2}}=3-{{x}^{2}}$ $\Rightarrow$ ${{x}^{2}}=3$ $\Rightarrow $ $x=\pm \sqrt{3}$ , $y=0$
Le curve di livello di $f$ sono un fascio di rette proprio $\frac{x-y+1}{x+3}=k$
Da cui: $x-y+1=k\left( x+3 \right)$. Il centro del fascio è dato dalla soluzione del sistema:
$\left\{ \begin{aligned} & x – y + 1 = 0 \\ & x + 3 = 0 \end{aligned} \right. \Rightarrow C = (-3, -2)$
Inoltre esplicitando l’equazione rispetto a $y$ si ha che $y=\left( 1-k \right)x+1-3k$ . Quindi il coefficiente angolare della retta è legata alla quota $k$ tramite $m=1-k$ . Quindi al crescere del coefficiente angolare diminuisce la quota della funzione.
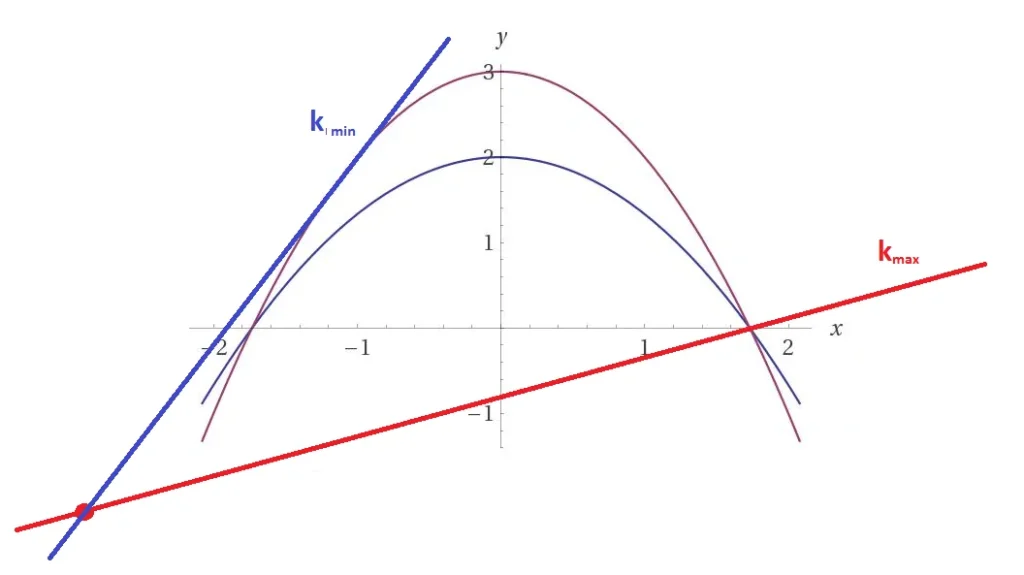
metodo delle curve di livello per individuare massimi e vinimi
La quota minima si ha per in corrispondenza della retta del fascio passante per il punto $\left( \sqrt{3},0 \right)$ . Quindi $\underset{\left( x,y \right)\in A}{\mathop{\max }}\,f={{k}_{\min }}=\frac{\sqrt{3}+1}{\sqrt{3}+3}=\frac{\sqrt{3}+1}{\sqrt{3}\left( 1+\sqrt{3} \right)}=\frac{1}{\sqrt{3}}$
La quota massima si in corrispondenza della retta tangente alla parabola più alta. Bisogna porre $y=\left( 1-k \right)x+1-3k$nell’equazione della parabola $y=3-{{x}^{2}}$e imporre $\Delta =0$ .
$\left( 1-k \right)x+1-3k=3-{{x}^{2}}\,\,\Rightarrow \,\,{{x}^{2}}+\left( 1-k \right)x-2-3k=0\,\,\,\Rightarrow \,\,\,$
$\Delta =1+{{k}^{2}}-2k+8+12k={{k}^{2}}+10k+9=0\,\,\Rightarrow \,\underset{\left( x,y \right)\in A}{\mathop{\min }}\,f=\,\,{{k}_{\min }}=-1$
ESERCIZIO 3
$f\left( x,y \right)=\log \left( x+1 \right)+\log \left( y+1 \right)$ su $A=\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}:\,\,{{x}^{2}}+{{y}^{2}}\le 4,x\ge 0,y\ge 0 \}$
L’insieme A è un arco circonferenza delimitato dai semiassi positivi delle ascisse e delle ordinate.
$f\left( x,y \right)=\log \left( x+1 \right)+\log \left( y+1 \right)=\log \left[ \left( x+1 \right)\left( y+1 \right) \right]$.
Il logaritmo è una funzione monotona, quindi le curve di livello della funzione $f\left( x,y \right)$ crescono nella stessa direzione in cui crescono quelle del suo argomento, cioè se ${{c}_{2}}>{{c}_{1}}\,\,\,\Rightarrow \,\,\,\log {{c}_{2}}>\log {{c}_{1}}$ .
Cerchiamo di capire cosa rappresentano le curve di livello dell’argomento del logaritmo:
$\left( x+1 \right)\left( y+1 \right)=c$ può essere vista come una traslazione del luogo geometrico definito in maniera implicita dall’equazione $xy=c$, di un vettore $v=\left( -1,-1 \right)$ .
$xy=c$ è una iperbole avente come asintoti gli assi cartesiani e posizionata nel primo e terzo quadrante se $c>0$, nel secondo e quarto quadrante $c<0$. Se invece $c=0$ l’iperbole degenera in due rette (asse x e asse y).
In particolare siamo interessati al caso $c>0$
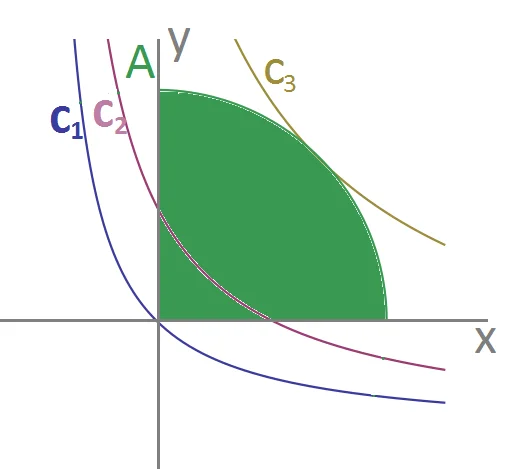
metodo delle curve di livello per individuare massimi e minimi
Al crescere di $c$ le curve di livello si spostano verso l’alto, e il vertice delle iperboli si sposta lungo la bisettrice del primo e terzo quadrante. Il massimo della funzione sull’insieme $A$ (tenendo presente l’andamento delle curve di livello in figura e le simmetrie del problema), si ha sulla circonferenza in coordinate ${{P}_{\max }}=\left( \sqrt{2},\,\,\sqrt{2} \right)$ e vale $f\left( {{P}_{\max }} \right)=\log \left( 5+\sqrt{2} \right)$ , mentre il minimo si trova nell’origine e vale $f\left( 0,0 \right)=0$
Esercizi su massimi e minimi in 2 variabili (Metodo della Parametrizzazione del bordo)
ESERCIZIO 4
Data la funzione $f\left( x,y \right)=y={{x}^{2}}+{{y}^{2}}-\frac{x}{2}$ cercare massimo e minimo assoluti della funzione su $C=\{{{x}^{2}}+{{y}^{2}}\le 1,\,\,\,{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}\le 1 \}$
L’insieme $C$ è costituito dall’interno di una circonferenza centrata nell’origine e di raggio unitario e l’esterno di una circonferenza di raggio unitario e centrata in $c=\left( 1,-1 \right)$ .
Cerchiamo i punti stazionari: $\nabla f=0$ :
$\left\{ \begin{aligned} & 2x – \frac{1}{2} = 0 \\ & 2y = 0 \end{aligned} \right. \Rightarrow P_0 = \left( \frac{1}{4}, 0 \right) \in C \Rightarrow f(P_0) = \frac{1}{16} – \frac{1}{8} = -\frac{1}{16}$
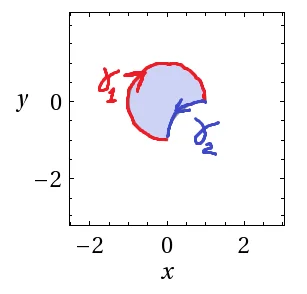
parametrizzazione del bordo e teorema di Weierstress per individuare massimi e minimi
Il bordo dell’insieme può essere parametrizzato con due archi di circonferenza ${{\gamma }_{1}}$ e ${{\gamma }_{2}}$.
Tra i potenziali massimi e minimi bisogna prendere in considerazione anche l’intersezione tra ${{\gamma }_{1}}$ e ${{\gamma }_{2}}$ in ${{P}_{1}}=\left( 0,-1 \right)$ e ${{P}_{2}}=\left( 1,0 \right)$.
Il bordo del primo arco di circonferenza può essere parametrizzato con ${{\gamma }_{1}}=\left( \cos t,\sin t \right)$, dove $t\in \left[ 0,\frac{3}{2}\pi \right]$.
${{\phi }_{1}}\left( t \right)=f\left( \cos t,\sin t \right)={{\cos }^{2}}t+{{\sin }^{2}}t-\frac{\cos t}{2}=1-\frac{\cos t}{2}$
${{\phi }_{1}}^{\prime }\left( t \right)=\frac{\sin t}{2}=0$ $\Rightarrow $ $t=\left\{ 0,\pi \right\}$
Per $t=0$ si ha ${{P}_{2}}=\left( \cos 0,\sin 0 \right)=\left( 1,0 \right)$ , $f\left( {{P}_{2}} \right)=\phi \left( 0 \right)=\frac{1}{2}$
Per $t=\pi $ si ha ${{P}_{3}}=\left( \cos \pi ,\sin \pi \right)=\left( -1,0 \right)$, $f\left( {{P}_{3}} \right)=\phi \left( \pi \right)=\frac{3}{2}$
$f\left( {{P}_{4}} \right)=\phi \left( \frac{3}{2}\pi \right)=1$
Il bordo del secondo arco di circonferenza può essere parametrizzato traslando la curva ${{\gamma }_{0}}=\left( \cos t,\sin t \right)\,\,\,t\in \left( \frac{\pi }{2},\pi \right)$ di un vettore$c=\left( 1,-1 \right)$. Quindi si ottiene la parametrizzazione ${{\gamma }_{2}}={{\gamma }_{0}}+c=\left( \cos t+1,\sin t-1 \right)\,\,\,\,\,t\in \left( \frac{\pi }{2},\pi \right)$ .
${{\phi }_{1}}\left( t \right)=f\left( \cos t+1,\sin t-1 \right)={{\left( \cos t+1 \right)}^{2}}+{{\left( \sin t-1 \right)}^{2}}-\frac{\cos t+1}{2}=$
${{\cos }^{2}}t+2\cos t+1+{{\sin }^{2}}t-2\sin t+1-\frac{1}{2}\cos t-\frac{1}{2}=3+\frac{3}{2}\cos t-2\sin t$
Derivando rispetto a $t$ si ha:
${{\phi }_{1}}^{\prime }\left( t \right)=-\frac{3}{2}\sin t-2\cos t=0\,\,\,\Rightarrow \,\,\,\frac{\sin t}{\cos t}=-\frac{4}{3}\,\,\,\,\Rightarrow \,\,\tan t=-\frac{4}{3}$
La tangente è negativa nel secondo e quarto quadrante. Noi siamo interessati in particolare alla soluzione nel secondo quadrante, perché $t\in \left( \frac{\pi }{2},\pi \right)$ .
Il vettore $\left( \cos t,\sin t \right)$ , si ottiene normalizzando il vettore $v=\left( -3,4 \right)$, quindi $\left( \cos t,\sin t \right)=\frac{v}{\left\| v \right\|}=\left( -\frac{3}{5},\frac{4}{5} \right)$ .
Senza calcolare esplicitamente $t$ , è possibile ricavare le coordinate del punto sostituendo il valore di seno e coseno in ${{\gamma }_{2}}=\left( \cos t+1,\sin t-1 \right)$. Quindi ${{P}_{4}}=\left( -\frac{3}{5}+1,\,\,\,\frac{4}{5}-1 \right)=\left( \frac{2}{5},-\frac{1}{5} \right)$
Da cui $f\left( {{P}_{4}} \right)=\frac{4}{5}$ .
Il minimo e massimo assoluti sono:
$\underset{\left( x,y \right)\in \,\,C}{\mathop{\min }}\,\,f\left( x,y \right)=-\frac{1}{16}\,\,\,,\,\,\,\underset{\left( x,y \right)\in \,\,C}{\mathop{\max }}\,\,f\left( x,y \right)=\frac{3}{2}\,\,$
Esercizi su massimi e minimi in 2 variabili per insiemi costituiti da vincoli (Moltiplicatori di Lagrange/parametrizzazione del vincolo come una curva)
ESERCIZIO 5
Si vuole individuare punti di massimo e minimo della funzione$f\left( x,y \right)={{x}^{2}}y$ , lungo il vincolo definito in maniera implicita dalla parabola di equazione: $g\left( x,y \right)={{x}^{2}}+2x-y-2=0$
SOLUZIONE 1 (MOLTIPLICATORI DI LAGRANGE)
$\left\{ \begin{aligned} & 2xy = \lambda (2x + 2) \\ & x^2 = -\lambda \\ & x^2 + 2x – y – 2 = 0 \end{aligned} \right.$
Il vincolo è una parabola, non è un insieme limitato e quindi non vale il teorema di Weierstress, e allora i stazionari che individueremo sulla curva come zeri del gradiente della funzione Lagrangiana, andranno confrontati con i limiti per $x \to +\infty$ e $x \to -\infty$.
Faccio un passaggio di semplificazione nel sistema:
$\left\{ \begin{aligned} & xy = -x^2(x+1) \\ & \lambda = -x^2 \\ & x^2 + 2x – y – 2 = 0 \end{aligned} \right.$
Soluzione 1:
$\left\{ \begin{aligned} & x = 0 \\ & \lambda = 0 \\ & x^2 + 2x – y – 2 = 0 \end{aligned} \right.$
$\left\{ \begin{aligned} & x = 0 \\ & \lambda = 0 \\ & y = -2 \end{aligned} \right.$
Quindi $ P_0 = (0, -2) $.
Soluzione 2:
$\left\{ \begin{aligned} & y = -x(x+1) \\ & \lambda = -x^2 \\ & x^2 + 2x – y – 2 = 0 \end{aligned} \right.$
$\left\{ \begin{aligned} & y = -x(x+1) \\ & \lambda = -x^2 \\ & 2x^2 + 3x – 2 = 0 \end{aligned} \right.$
Il secondo sistema a sua volta ha due soluzioni:
$\left\{ \begin{aligned} & y = -\frac{3}{4} \\ & \lambda = -\frac{1}{4} \\ & x = \frac{1}{2} \end{aligned} \right. \quad \text{o} \quad \left\{ \begin{aligned} & y = -2 \\ & \lambda = -4 \\ & x = -2 \end{aligned} \right.$
Quindi $ P_1 = (-2, -2) $ e $ P_2 = \left(\frac{1}{2}, -\frac{3}{4}\right) $.
Infine, calcolando i valori della funzione $ f(x, y) $ nei punti $ P_0 $, $ P_1 $ e $ P_2 $ otteniamo:
$ f(0, -2) = 0, \quad f(-2, -2) = -8, \quad f\left(\frac{1}{2}, -\frac{3}{4}\right) = -\frac{3}{16} $
E l’andamento della funzione quando $ (x, y) $ tende all’infinito è $ +\infty $.
Si ha che ${{P}_{1}}$ è minimo assoluto, ${{P}_{0}}$è massimo relativo e ${{P}_{2}}$ è minimo relativo. Massimo assoluto non esiste perché la funzione va ad infinito percorrendo la parabola verso l’alto.
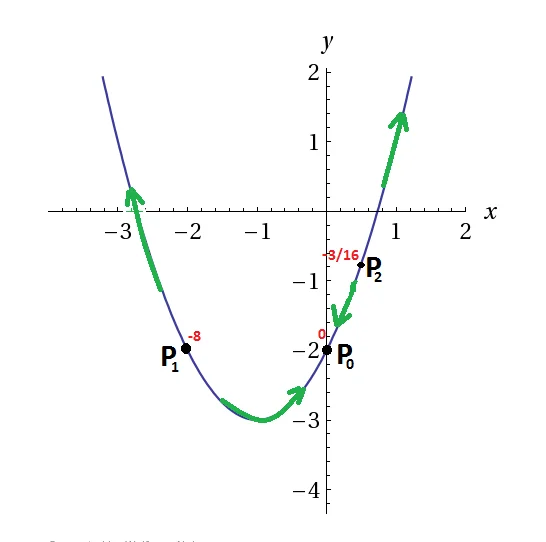
SOLUZIONE 2: PARAMETRIZZAZIONE DELLA PARABOLA
$f\left( x,y \right)={{x}^{2}}y$
$g\left( x,y \right)={{x}^{2}}+2x-y-2=0$
$y={{x}^{2}}+2x-2$
$\phi \left( x \right)=f\left( x,{{x}^{2}}+2x-2 \right)={{x}^{2}}\left( {{x}^{2}}+2x-2 \right)={{x}^{4}}+2{{x}^{3}}-2{{x}^{2}}$
${\phi }’\left( x \right)=4{{x}^{3}}+6{{x}^{2}}-4x=2x\left( 2{{x}^{2}}+3x-2 \right)=0,\,\,\,\Rightarrow \,\,{{x}_{0}}=-2\,\,,\,\,\,{{x}_{1}}=0,\,\,\,{{x}_{2}}=\frac{1}{2}$
$\underset{x\to \pm \infty }{\mathop{\lim }}\,\phi \left( x \right)=+\infty $,$\phi \left( -2 \right)=-8$, $\phi \left( 0 \right)=0$,$\phi \left( \frac{1}{2} \right)=-\frac{3}{16}$
ESERCIZIO 6
Individuare massimi e minimi assoluti di$f\left( x,y \right)={{e}^{{{x}^{2}}+2xy-{{y}^{2}}}}$ sul vincolo $C=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}:\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{6}=1 \right\}$
SOLUZIONE
Poiché l’esponenziale è una funzione monotona su tutto l’asse dei reali allora cercare massimi e minimi di $f\left( x,y \right)$ è lo stesso che cercare massimi e minimi di ${{f}_{1}}\left( x,y \right)={{x}^{2}}+2xy-{{y}^{2}}$
La Lagrangiana della funzione${{f}_{1}}\left( x,y \right)$ sull’insieme $C$ diventa $\Lambda \left( x,y,\lambda \right)={{x}^{2}}+2xy-{{y}^{2}}-\lambda \left( \frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{6}-1 \right)$ .
Ponendo $\nabla \Lambda =0$ si ottiene il sistema:
$\left\{ \begin{aligned} & 2x+2y = \lambda \frac{x}{2} \\ & 2x-2y = \lambda \frac{y}{3} \\ & \frac{x^2}{4} + \frac{y^2}{6} = 1 \end{aligned} \right.$
Riorganizzando le prime due equazioni, otteniamo:
$\left\{ \begin{aligned} & (4-\lambda)x + 4y = 0 \\ & 6x – (\lambda + 6)y = 0 \\ & 3x^2 + 2y^2 = 12 \end{aligned} \right.$
Le prime due equazioni costituiscono un sistema lineare omogeneo $\mathbf{Ax}=\mathbf{0}$ , dove $\mathbf{A}$ è data da:
$\mathbf{A}=\left[ \begin{matrix}4-\lambda & 4 \\6 & -\lambda -6 \\\end{matrix} \right]$
Il sistema ammette soluzione se $\det \mathbf{A}=0$ , oppure $x=y=0$ . La seconda soluzione è da scartare perché non appartiene al vincolo $C$.
$\det \mathbf{A}={{\lambda }^{2}}+2\lambda -48=0\,\,\,\,\Rightarrow \,\,\,\,{{\lambda }_{1,2}}=\left\{ -8,6 \right\}$ . Da cui:
$\left\{ \begin{aligned} & \lambda = 6 \\ & -2x + 4y = 0 \\ & 3x^2 + 2y^2 = 12 \\ \end{aligned} \right.$
Da cui:
$\left\{ \begin{aligned} & \lambda = 6 \\ & x = 2y \\ & 14y^2 = 12 \\ \end{aligned} \right.$
${{P}_{0}}=\left( 2\sqrt{\frac{6}{7}},\sqrt{\frac{6}{7}} \right),{{P}_{1}}=\left( -2\sqrt{\frac{6}{7}},-\sqrt{\frac{6}{7}} \right)f\left( {{P}_{0}} \right)=f\left( {{P}_{1}} \right)={{e}^{6}}$
$\left\{ \begin{aligned} & \lambda = -8 \\ & 12x + 4y = 0 \\ & 3x^2 + 2y^2 = 12 \\ \end{aligned} \right.$
Da cui:
$\left\{ \begin{aligned} & \lambda = -8 \\ & y = -3x \\ & 21x^2 = 12 \\ \end{aligned} \right.$
Da cui:
$\begin{aligned} &P_2=\left( \frac{2}{\sqrt{7}},-\frac{6}{\sqrt{7}} \right), \\ &P_3=\left( -\frac{2}{\sqrt{7}},\frac{6}{\sqrt{7}} \right), \\ &f\left( P_2 \right)=f\left( P_3 \right)=e^{-8}\end{aligned}$
L’insieme $C$essendo rappresentato da un ellissi è chiuso e limitato e la funzione e continua su di esso e per Weierstress massimo e minimo esistono sicuramente e valgono $\underset{C}{\mathop{\max }}\,f\left( x,y \right)={{e}^{6}}$ e $\underset{C}{\mathop{\min }}\,f\left( x,y \right)={{e}^{-8}}$.
Le curve di livello della funzione $f\left( x,y \right)$ si ottengono ponendo costante l’esponente e sono delle iperboli.
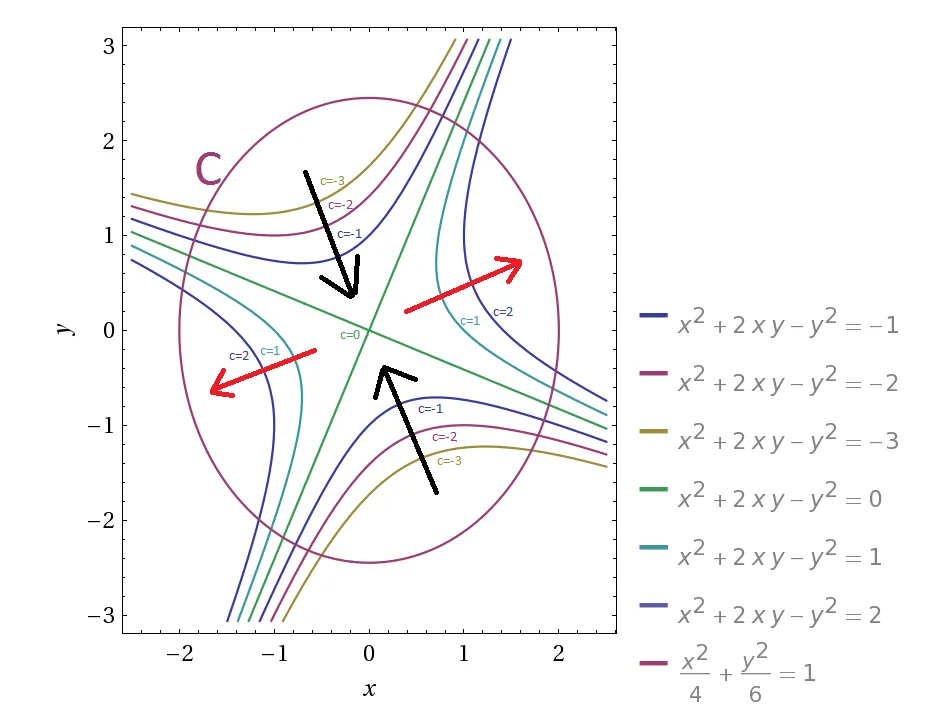
Il massimo e minimo della funzione su $C$ si hanno laddove l’ellissi risulta tangente all’iperbole. Quindi data la simmetria iperbolica della funzione si ha che ammette due massimi e due minimi.