Indice dei contenuti
- PROBLEMA 1
- PROBLEMA 2
- QUESTIONARIO
- SOLUZIONE PROBLEMA 1
- SOLUZIONE PROBLEMA 2
- SOLUZIONE QUESITI
- Soluzione quesito 1 della Simulazione Maturità Scientifica dicembre 2019 Matematica
- Soluzione quesito 2 della Simulazione Maturità Scientifica dicembre 2019 Matematica
- Soluzione quesito 3 della Simulazione Maturità Scientifica dicembre 2019 Matematica
- Soluzione quesito 4 della Simulazione Maturità Scientifica dicembre 2019 Matematica
- Soluzione quesito 5 della Simulazione Maturità Scientifica dicembre 2019 Matematica
- Soluzione quesito 6 della Simulazione Maturità Scientifica dicembre 2019 Matematica
- Soluzione quesito 7 della Simulazione Maturità Scientifica dicembre 2019 Matematica
- Soluzione quesito 8 della Simulazione Maturità Scientifica dicembre 2019 Matematica
Si riporta il testo integrale e la Soluzione della Simulazione Maturità Scientifica dicembre 2019 Matematica:
PROBLEMA 1
Fissati due parametri reali 𝑆>0,𝑘>0, considera la funzione:
\(f_k(x)=\frac{S}{1+e^{-kx}}\), il cui grafico viene indicato con \(\Gamma_k\).
La funzione \(f_k(x)\). può essere adoperata per studiare la possibile evoluzione nel tempo di una popolazione che abbia capacità di riprodursi, nell’ipotesi in cui la limitatezza delle risorse disponibili causi l’esistenza di una “soglia di sostenibilità” al di sotto della quale la popolazione è costretta a mantenersi.
1. Dimostra che i valori assunti dalla funzione \(f_k(x)\) si mantengono all’interno dell’intervallo aperto delimitato inferiormente dal valore 0 e superiormente dal valore S, dove quest’ultimo rappresenta tale soglia di sostenibilità.
2. Osservando \(\Gamma_k\), individua la trasformazione geometrica da applicare a \(\Gamma_k\) per farlo diventare il grafico di una funzione dispari, e determina l’espressione analitica di tale funzione.
3. Individua graficamente o analiticamente il valore della x corrispondente alla massima velocità di crescita di una popolazione secondo il modello rappresentato dalla funzione \(f_k(x)\); determina quindi, in funzione dei parametri S e k, il valore di tale velocità massima.
Dovendo effettuare lo studio di una coltura batterica in un ambiente a risorse limitate, puoi pensare, al fine di semplificare i calcoli, di approssimare la funzione \(f_k(x)\) con una funzione come \(g_k(x)\), il cui grafico è riportato nella figura seguente:
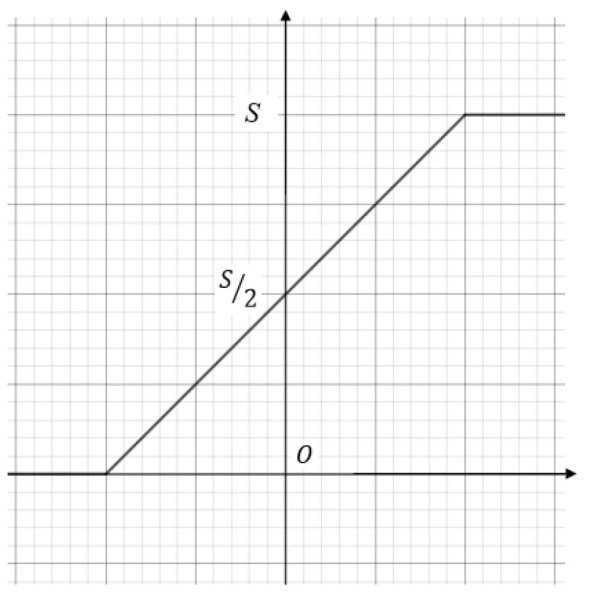
Il valore di \(g_k(x)\) passa da 0 a S con una rampa lineare, di pendenza pari alla pendenza di \(\Gamma_k\)nel punto di ascissa 0.
4. Determina, in funzione dei parametri S e k, l’espressione analitica della funzione \(g_k(x)\).
5. Illustra il procedimento che adotteresti per valutare la accettabilità dell’approssimazione di \(f_k(x)\) fornita da \(g_k(x)\).
6. All’aumentare di k, tale approssimazione diventa migliore? Motiva la tua risposta.
Soluzione Problema 1 – Simulazione prova di Matematica – dicembre 2019
PROBLEMA 2
Il tuo liceo, nell’ambito dell’alternanza scuola lavoro, ha organizzato per gli studenti del quinto anno un’attività presso lo stabilimento ICE EXPRESS sito nella tua regione. All’arrivo siete stati divisi in vari gruppi. Il tuo, dopo aver visitato lo stabilimento e i laboratori, partecipa ad una riunione legata ai processi di produzione.
Un cliente ha richiesto una fornitura di blocchi di ghiaccio a forma di parallelepipedo a base quadrata, di volume 10 \(dm^3\), che abbiano il minimo scambio termico con l’ambiente esterno, in modo da resistere più a lungo possibile prima di liquefarsi.
Al tuo gruppo viene richiesto di determinare le caratteristiche geometriche dei blocchi da produrre, sapendo che gli scambi termici tra questi e l’ambiente avvengono attraverso la superficie dei blocchi stessi.
1. Determina il valore del lato b della base quadrata che consente di minimizzare lo scambio termico e il corrispondente valore dell’altezza h, tenendo presente la necessità che il volume sia \(dm^3\).
Il blocco di ghiaccio al termine del processo produttivo si trova alla temperatura di -18°C. Esso viene posto su un nastro trasportatore che lo porta a un camion frigorifero, attraversando per due minuti un ambiente che viene mantenuto alla temperatura di 10°C; esso pertanto tende a riscaldarsi, con velocità progressivamente decrescente, in funzione della differenza di temperatura rispetto all’ambiente, e inizia a fondere se lungo il percorso raggiunge la temperatura di 0°C.
2. Scegli, motivando la tua scelta, quale delle seguenti funzioni è più idonea per rappresentare il processo di riscaldamento prima dell’inizio della liquefazione (\(T_a \)= temperatura ambiente, \(T_g \)= temperatura del ghiaccio all’istante \(t = 0\) , \(T(t) = \) temperatura del ghiaccio all’istante t, dove t è il tempo trascorso dall’inizio del riscaldamento, in minuti):\[𝑇(𝑡)=(𝑇_𝑎−𝑇_𝑔) \cdot 𝑒^{−𝐾𝑡} \] \[𝑇(𝑡)=(𝑇_𝑎−𝑇_𝑔) \cdot (1−𝑒^{−𝐾𝑡})+𝑇_𝑔 \] \[𝑇(𝑡)=(𝑇_𝑎−𝑇_𝑔)\cdot 𝑒^{𝐾𝑡}−𝑇_𝑎\]
e determina il valore che deve avere il parametro K perché il blocco di ghiaccio non inizi a fondere durante il percorso verso il camion frigorifero.
3. Poiché il parametro K varia in funzione di diversi fattori produttivi, c’è un’incertezza del 10% sul suo effettivo valore. Ritieni che questo determini una incertezza del 10% anche sul valore della temperatura T del blocco di ghiaccio all’istante in cui raggiunge il camion frigorifero? Motiva la tua risposta, in modo qualitativo o quantitativo.
L’azienda solitamente adopera, per contenere l’acqua necessaria a produrre un singolo blocco di ghiaccio, un recipiente cilindrico, con raggio della base eguale a 1,5 dm, e altezza eguale a 2 dm.
4. Sapendo che nel passaggio da acqua a ghiaccio il volume aumenta del 9,05%, stabilisci se il suddetto recipiente è in grado di contenere l’acqua necessaria a produrre il blocco richiesto e, in tal caso, a quale altezza dal fondo del recipiente arriverà l’acqua.
Soluzione Problema 2 – Simulazione prova di Matematica – dicembre 2019
QUESTIONARIO
QUESITO 1
In figura è riportato il grafico della funzione \(𝑓′(𝑥)\), derivata della funzione \(𝑓(𝑥)\). Il grafico presenta un asintoto verticale per \(𝑥=0\). Supponendo che la funzione \(𝑓\) sia definita in ℝ, descrivi la derivabilità della funzione nel punto di ascissa nulla e fornisci un grafico probabile della funzione in un intorno di zero.
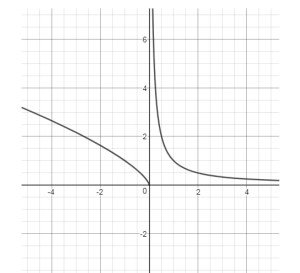
Soluzione Quesito 1 – Simulazione prova di Matematica – dicembre 2019
QUESITO 2
Individua il valore di k per cui la tangente nell’origine al grafico della funzione
\[f(x)=\frac{x}{x-k}\]
forma un angolo di 𝜋/6 radianti con l’asse delle ascisse.
Soluzione Quesito 2 – Simulazione prova di Matematica – dicembre 2019
QUESITO 3
Risolvi esclusivamente per via grafica la disequazione:
$|𝑥 − 2| > |𝑥 − 6|$
Soluzione Quesito 3 – Simulazione prova di Matematica – dicembre 2019
QUESITO 4
Il cerchio di raggio R centrato nel vertice in basso a sinistra del quadrato in figura ne ricopre metà della superficie; il cerchio di raggio r centrato nel centro del secondo quadrato ne occupa metà della superficie. Sapendo che i quadrati sono equivalenti, determina il rapporto R/r.

Soluzione Quesito 4 – Simulazione prova di Matematica – dicembre 2019
QUESITO 5
Presi due punti \(𝐴(𝑎,𝑎^2)\) e \(𝐵(𝑏,𝑏^2)\) sulla parabola \(𝑦=𝑥^2\) , traccia la retta \(OC\), parallela alla retta \(AB\) e passante per l’origine e per il punto \(𝐶(𝑐,𝑐^2)\).

Dimostra che \(a+b=c\)
Traccia un’altra parallela \(DE\), passante per due punti D ed E appartenenti alla parabola, e mostra che i punti medi delle tre parallele giacciono su una retta.
Soluzione Quesito 5 – Simulazione prova di Matematica – dicembre 2019
QUESITO 6
Il grafico della funzione polinomiale cubica \(𝑦=𝑓(𝑥)\) intercetta l’asse x nei punti di ascissa 10, 100 e 1000. È sufficiente questa informazione per individuare le coordinate del punto di flesso? Se sì, determinale. Se no, spiega per quale motivo.
Soluzione Quesito 6 – Simulazione prova di Matematica – dicembre 2019
QUESITO 7
Una sfera, il cui centro è il punto 𝐾(1,0,1), è tangente al piano Π avente equazione \(𝑥−2𝑦+𝑧+1=0\). Qual è il punto di tangenza? Qual è il raggio della sfera?
Soluzione Quesito 7 – Simulazione prova di Matematica – dicembre 2019
QUESITO 8
Se si lancia una moneta 2 volte, la probabilità di ottenere una testa e una croce (in qualsiasi ordine) è pari al 50%. Se la moneta viene lanciata 4 volte, la probabilità di ottenere due teste e due croci, in qualsiasi ordine, è ancora pari al 50%? Motiva la tua risposta.
Soluzione Quesito 8 – Simulazione prova di Matematica – dicembre 2019
Clicca per le altre simulazioni per la maturità scientifica.
SOLUZIONE PROBLEMA 1
Soluzione domanda 1
Per fare ciò possiamo semplicemente verificare che la disequazione \(0<{{f}_{k}}(x)<S\) è sempre verificata.
\({{f}_{k}}(x)>0\) è sempre verificata, visto che sia al numeratore che al denominatore compaiono soltanto termini positivi.
\( {{f}_{k}}(x)<S\) \(\Rightarrow \)\(\frac{S}{1+{{e}^{-kx}}}<S\)\(\Rightarrow \)\(\frac{1}{1+{{e}^{-kx}}}<1\)\(\Rightarrow \)\(1<1+{{e}^{-kx}}\)\(\Rightarrow \)\({{e}^{-kx}}>0\)
Anche la seconda disequazione è sempre verificata visto che sia l’esponenziale che il fattore che k sono quantità positive \(\forall x\in \mathbb{R}\)
2. Osservando \(\Gamma_k\), individua la trasformazione geometrica da applicare a \(\Gamma_k\) per farlo diventare il grafico di una funzione dispari, e determina l’espressione analitica di tale funzione.
Soluzione domanda 2
Affinchè Γ𝑘 diventi il grafico di una funzione dispari, si deve avere che \({{f}_{k}}\left( -x \right)=-{{f}_{k}}(x)\) \(\forall x\in \mathbb{R}\), dove \(\mathbb{R}\) coincide con il dominio della funzione.
Lasciando inalterato il grafico per x>0, vogliamo che per le x negative valga la relazione per le funzioni dispari.
Per fare ciò possiamo scrivere:
$${{g}_{k}}\left( x \right)=\left\{ \begin{array}{ll}{{f}_{k}}(x) & \text{se } x>0 \\0 & \text{se } x=0 \\-{{f}_{k}}(-x) & \text{se } x<0 \\\end{array} \right.$$
Il cui grafico si costruisce facilmente osservando che per x>0 la funzione è monotona crescente, essendo proporzionale al reciproco di una funzione monotona decrescente.
Inoltre sappiamo che \(0<{{f}_{k}}(x)<S\), possiamo verificare che \(\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,{{f}_{k}}(x)=1\) e che \(\underset{x\to \infty }{\mathop{\lim }}\,{{f}_{k}}(x)=S\). Quindi per x>0 si tratta di una funzione crescente che parte da 1+ e cresce avvicinandosi indefinitamente al valore S senza mai raggiungerlo. Per x<0 è possibile invece specchiare la funzione rispetto all’origine.
Soluzione domanda 3
La massima crescita si ha quando è massima la derivata della funzione \(f_k(x)\). Per fare ciò studiamo il segno della derivata seconda:
\(\frac{d{{f}_{k}}(x)}{dx}=\frac{kS\,{{e}^{-kx}}}{{{\left( 1+{{e}^{-kx}} \right)}^{2}}}\)
\(\frac{{{d}^{2}}{{f}_{k}}(x)}{d{{x}^{2}}}={{k}^{2}}{{e}^{-kx}}\frac{{{e}^{-kx}}-1}{{{\left( 1+{{e}^{-kx}} \right)}^{3}}}>0\)\(\Rightarrow \)\({{e}^{-kx}}-1>0\)\(\Rightarrow \)\({{e}^{-kx}}>1\)\(\Rightarrow \)\(x<0\)
Dallo studio del segno della derivata seconda si evince che la derivata della funzione \(𝑓_𝑘(𝑥)\), ha un massimo in corrispondenza di x=0, in corrispondenza del quale si incontra il punto di massima crescita della funzione.
La velocità massima è data dalla derivata della funzione calcolata nell’origine.
\(\frac{d{{f}_{k}}(0)}{dx}=\frac{kS\,}{4}\)
Dovendo effettuare lo studio di una coltura batterica in un ambiente a risorse limitate, puoi pensare, al fine di semplificare i calcoli, di approssimare la funzione \(f_k(x)\) con una funzione come \(g_k(x)\), il cui grafico è riportato nella figura seguente:
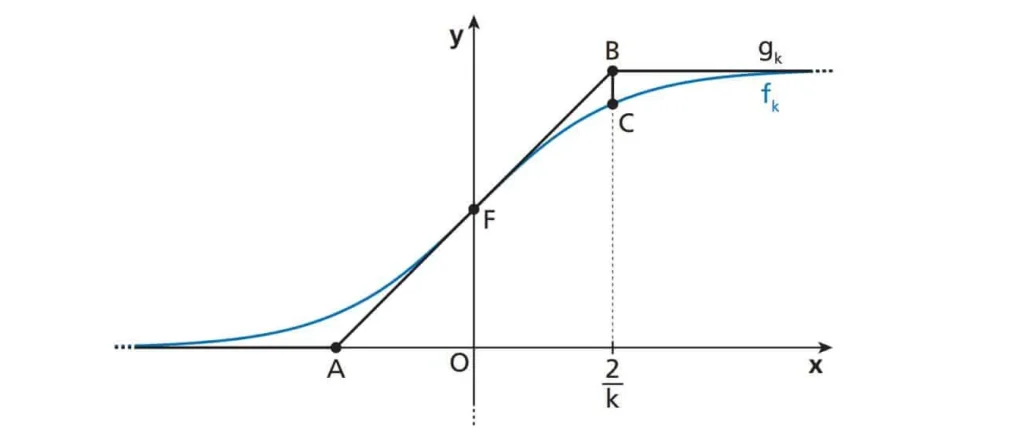
Il valore di \(g_k(x)\) passa da 0 a S con una rampa lineare, di pendenza pari alla pendenza di \(\Gamma_k\)nel punto di ascissa 0.
Soluzione domanda 4
La funzione \(g_k(x)\) può essere definita come una funzione a tratti.
In particolare tale funzione è una retta con pendenza \(\frac{d{{f}_{k}}(0)}{dx}=\frac{kS\,}{4}\), e passante per il punto P=(0,S/2). Quindi otteniamo che il coefficiente angolare della retta è \(m=\frac{kS\,}{4}\), mentre l’intercetta con le ordinate è \(q=\frac{S\,}{2}\).
La retta \(y=\frac{kS\,}{4}x+\frac{S\,}{2}\) intercetta l’asse x in \(\frac{kS\,}{4}x+\frac{S\,}{2}=0\)\(\Rightarrow \)\(x=-\frac{2}{k}\).
La retta \(y=\frac{kS\,}{4}x+\frac{S\,}{2}\) intercetta l’asintoto della funzione f𝑘(𝑥) di equazione y=S in \(\frac{kS\,}{4}x+\frac{S\,}{2}=S\)\(\Rightarrow \)\(x=\frac{2}{k}\).
E per finire scriviamo la funzione:
$${{g}_{k}}\left( x \right)=\left\{ \begin{array}{ll}S & \text{se } x \geq \frac{2}{k} \\\frac{kS}{4}x + \frac{S}{2} & \text{se } -\frac{2}{k} \leq x < \frac{2}{k} \\0 & \text{se } x < -\frac{2}{k} \\\end{array} \right.$$
Soluzione domanda 5
Definiamo la funzione errore $e_k(x) = |g_k(x) – f_k(x)|$.
Si osserva che i grafici sono entrambi simmetrici rispetto al punto F, pertanto possiamo studiare il massimo della funzione errore soltanto per $x > 0$, e varrà lo stesso per $x < 0$.
$$e_k(x) = \left\{\begin{array}{ll}S – f_k(x) & \text{se } x \geq \frac{2}{k} \\\frac{kS}{4}x + \frac{S}{2} – f_k(x) & \text{se } 0 \leq x < \frac{2}{k}\end{array}\right.$$
Calcolo la derivata prima di $e_k(x)$ e ne studio il segno:
$${e_k}'(x) = \left\{\begin{array}{ll}- f_k'(x) & \text{se } x \geq \frac{2}{k} \\\frac{kS}{4} – f_k'(x) & \text{se } 0 \leq x < \frac{2}{k}\end{array}\right.$$
Si sa che \({{f}_{k}}^{\prime }(x)>0\) è sempre positiva osservando la sua espressione calcolata nel punto 3. \(-{{f}_{k}}^{\prime }(x)<0\) e di conseguenza l’errore tende a diminuire per x>2/k.
Inoltre, studiando la funzione ek(x) nell’intervallo tra 0 e 2/k, si può osservare che la sua derivata in tale intervallo vale:
\({{e}_{k}}^{\prime }(x)=kS\left( \frac{{{\left( 1+{{e}^{-kx}} \right)}^{2}}-4{{e}^{-kx}}}{4{{\left( 1+{{e}^{-kx}} \right)}^{2}}} \right)\)
Studiandone il segno in tale intervallo \({{e}_{k}}^{\prime }(x)>0\) si ha:
\({{\left( 1+{{e}^{-kx}} \right)}^{2}}-4{{e}^{-kx}}>0\) \(\Rightarrow \) \({{e}^{-2kx}}-2{{e}^{-kx}}+1>0\)\(\Rightarrow \)\({{\left( {{e}^{-kx}}-1 \right)}^{2}}>0\)
Possiamo dedurre che la derivata della funzione errore è positiva nell’intervallo tra 0 e 2/k, e quindi l’errore tende ad aumentare in questo intervallo.
Possiamo concludere che il massimo di tale funzione si trova in corrispondenza di x=2/k.
L’errore massimo commesso approssimando \(g_𝑘(𝑥)\) fornita da \(f_𝑘(𝑥)\) è:
\({{e}_{MAX}}={{e}_{k}}(2/k)\cong 0,12S\)
Si può osservare che quest’ultimo dipende dal parametro S ma non da k.
Per concludere possiamo valutare l’errore relativo in corrispondenza del punto di massimo e usarlo come indice di bontà dell’approssimazione fatta.
\({{E}_{rel}}=\frac{{{e}_{k}}(2/k)}{{{f}_{k}}(2/k)}={{e}^{-2}}\cong 0,14\)
Soluzione domanda 6
Al variare di k, quindi, il valore massimo dello scarto tra la funzione esatta e la sua approssimazione rimane costante; possiamo dunque concludere che la qualità dell’approssimazione resta costante quando k varia, in particolare quando k cresce, in base al criterio scelto per confrontare le due funzioni.
Un metodo alternativo e più preciso per affrontare i punti 5. e 6. era quello di scegliere un criterio diverso per confrontare le funzioni. Potevamo scegliere di utilizzare l’errore medio, che si otteneva calcolando l’area compresa tra i due grafici oppure di valutare l’errore quadratico medio.
SOLUZIONE PROBLEMA 2
Soluzione domanda 1
Si tratta di un problema di ottimizzazione vincolata, dove il volume del parallelepipedo a base quadrata, costituisce il vincolo:
\(V={{b}^{2}}h=10\,\) \(\Rightarrow \)\(h=\frac{10\,}{{{b}^{2}}}\)
Mentre la superficie del blocco di ghiaccio è la quantità da minimizzare, per ridurre al minimo lo scambio termico:
\(S=2{{S}_{base}}+{{S}_{laterale}}=2{{b}^{2}}+4bh=2{{b}^{2}}+\frac{40}{b}\)
Il punto di minimo si ottiene dallo studio del segno della derivata prima calcolata rispetto a b
\({S}’=4b-\frac{40}{{{b}^{2}}}>0\)\(\Rightarrow \)\(4{{b}^{3}}-40>0\)\(\Rightarrow \)\(b>\sqrt[3]{10}\)
Pertanto la minima superficie che consente il minimo scambio termico si ha se
\(b=h=\sqrt[3]{10}\,d{{m}^{3}}\)
Quindi scegliendo come forma geometrica un cubo (caso particolare di parallelepipedo) Il blocco di ghiaccio al termine del processo produttivo si trova alla temperatura di -18°C. Esso viene posto su un nastro trasportatore che lo porta a un camion frigorifero, attraversando per due minuti un ambiente che viene mantenuto alla temperatura di 10°C; esso pertanto tende a riscaldarsi, con velocità progressivamente decrescente, in funzione della differenza di temperatura rispetto all’ambiente, e inizia a fondere se lungo il percorso raggiunge la temperatura di 0°C.
Soluzione domanda 2
La temperatura iniziale deve essere di -18°, quindi la funzione deve innanzi tutto rispettare la condizione T(0)= – 18.
L’unica funzione che rispetta questa condizione è la seconda funzione
𝑇(𝑡)=(𝑇𝑎−𝑇𝑔)(1−e-Kt) + 𝑇𝑔 = 10 – 28 e-Kt
A questo punto verifichiamo se la funzione individuata rispetta anche gli altri requisiti:
Deve riscaldarsi con velocità progressivamente, vuol dire che la funzione cercata deve essere monotona crescente T’>0 e concava T’’<0.
𝑇’(𝑡)= 28 K e-Kt >0 per qualunque valore di t se K>0
𝑇’’(𝑡)= -K2 28 e-Kt <0 per qualunque valore di t.
Inoltre in un tempo infinito deve raggiungere la temperatura limite di 10°C. Vuol dire che per \(t\to \infty \) si deve avere che \(T(t)\to 10\), e anche questo è verificato infatti
\(\underset{t\to \infty }{\mathop{\lim }}\,T(t)=10\) se K>0.
Per finire determiniamo il valore di K, affinché il ghiaccio non inizi a fondere durante il percorso, ovvero T(t)<0 nell’ intervallo tra 0 e 2. Si tratta di una funzione monotona crescente, quindi per risolvere il problema andiamo a confrontare l’istante in cui la temperatura è massima con 0°.
Si deve avere T(2)<0 \(\Rightarrow \) 10 – 28 e-Kt <0 \(\Rightarrow \)\(K<\ln \sqrt{\frac{14}{5}}\)
Per cui i valori di K ammissibili per la funzione sono:
\(0<K<\ln \sqrt{\frac{14}{5}}\)
Soluzione domanda 3
La temperatura con cui il ghiaccio raggiunge il camion è quella che si ottiene per t=2, si può esprimere in funzione di k e vale \(T(K)=10-28\,{{e}^{-2K}}\)
Si ha quindi che pe un qualunque valore di K, il valore effettivo è compreso nell’intervallo \([K-0.1K\,\,,\,\,\,K+0.1K]=[0.9K\,\,,\,\,1.1K]\)
All’interno di questo intervallo la temperatura di arrivo al camioncino varia nell’intervallo \([T(0.9K)\,\,,\,T(\,1.1K)]=[10-28\,{{e}^{-1.8K}},10-28\,{{e}^{-2.2K}}]\) e la variazione di temperatura all’interno di questo intervallo è pari a
\(\Delta T = T(0.9K) – T(1.1K) = 28(e^{-2.2K} – e^{-1.8K})\)
La temperatura di arrivo sarà pari al più pari a \(T(1.1K)\) con un errore relativo rispetto al valore atteso di \({{E}_{1}}(K)=\frac{T(1.1K)-T(K)}{T(K)}\).
La minima temperatura di arrivo invece sarà pari a \(T(0.9K)\) con un errore relativo rispetto al valore atteso di \({{E}_{2}}(K)=\frac{T(0.9K)-T(K)}{T(K)}\).
L’incertezza di misura può essere calcolata come il massimo errore percentuale commesso al variare di K, ovvero \(E(K)=\max \left\{ \left| {{E}_{1}}(K) \right|,\left| {{E}_{2}}(K) \right| \right\}\), dove l’incertezza può essere interpretata come “L’errore percentuale massimo che si ha rispetto alla temperatura di arrivo, in funzione del valore di K scelto”.
Attraverso uno studio dettagliato della funzione E(K) nell’intervallo \(0<K<\ln \sqrt{\frac{14}{5}}\), è possibile studiare come varia l’incertezza della temperatura di arrivo al furgoncino al variare di K.
Lo studio della funzione E(K) non è necessario per rispondere alla domanda.
Supponiamo di scegliere un valore di K=0.4 che si trova all’interno dell’intervallo considerato.
\({{E}_{1}}(0.4)=\frac{T(0.44)-T(0.4)}{T(0.4)}=\frac{-1.614+2.581}{2.581}=0.375\)
Quindi per K=0.4 posso ottenere una temperatura di arrivo che risulta del 37.5% maggiore rispetto a quella prevista, che supera quasi di 4 volte l’errore percentuale del 10% massimo che posso avere sul valore di K.
Per concludere, possiamo dire che l’incertezza della temperatura di arrivo dei cubi di ghiaccio è una funzione che dipende da K, e che ci sono valori di K (ad esempio K=0.4) per cui l’incertezza può essere molto diversa rispetto all’incertezza di K.
L’azienda solitamente adopera, per contenere l’acqua necessaria a produrre un singolo blocco di ghiaccio, un recipiente cilindrico, con raggio della base eguale a 1,5 dm, e altezza eguale a 2 dm.
Soluzione domanda 4
\({{V}_{Blocco}}=10\,d{{m}^{3}}\)
\({{V}_{Acqua}}=\frac{{{V}_{Blocco}}}{1.0905}=9,17\,d{{m}^{3}}\)
\({{V}_{Cilindro}}=\pi {{r}^{2}}h\simeq 14,14\,d{{m}^{3}}\)
\({{h}_{Acqua}}=\frac{{{V}_{Acqua}}}{\pi {{r}^{2}}}\simeq 1,3\,dm<2dm\)
SOLUZIONE QUESITI
Soluzione quesito 1 della Simulazione Maturità Scientifica dicembre 2019 Matematica
Per prima cosa possiamo dedurre dal grafico e dal testo i limiti destro e sinistro della derivata prima della funzione f(x) e si avrà:
\(\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,{f}'(x)=0\)
\(\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,{f}'(x)=+\infty \)
Possiamo dedurre che il grafico della funzione f(x) ha tangente orizzontale a sinistra di zero e ha tangente verticale a destra di zero.
La funzione è se mpre crescente visto che f’(x) è tutta positiva.
La funzione è sempre concava perché essendo f’(x) decrescente si avrà che f’’(x) è negativa per ogni valore di x
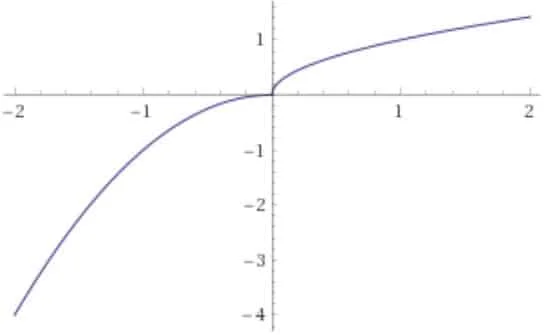
Soluzione quesito 2 della Simulazione Maturità Scientifica dicembre 2019 Matematica
Per prima cosa osserviamo che la funzione interseca l’ascissa nell’origine degli assi O.
La derivata prima fornisce il coefficiente angolare della retta tangente al grafico in corrispondenza del punto in cui essa viene calcolata. Il coefficiente angolare è pari alla tangente dell’angolo che tale retta forma con l’ascissa.
Nel nostro caso abbiamo che l’angolo è \(\frac{\pi }{6}\), la cui tangente vale \(\frac{1}{\sqrt{3}}\).
Quindi bisogna imporre che nell’origine la derivata della funzione deve essere uguale alla tangente di \(\frac{\pi }{6}\) , quindi \({f}'(0)=\frac{1}{\sqrt{3}}\).
La derivata della funzione vale
\({f}'(x)=\frac{-k}{{{\left( x-k \right)}^{2}}}\)
Sostituendo x=0 si ha
\({f}'(0)=\frac{-1}{k}=\frac{1}{\sqrt{3}}\)\(\Rightarrow \)\(k=-\sqrt{3}\)
Soluzione quesito 3 della Simulazione Maturità Scientifica dicembre 2019 Matematica
Partiamo dal disegnare sullo stesso grafico le due funzioni.
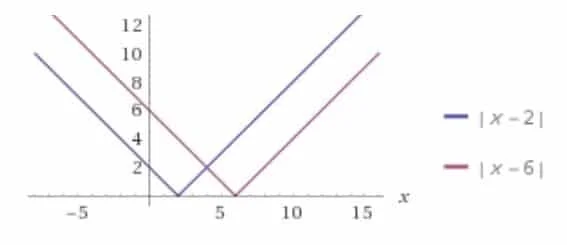
Per risolvere graficamente la disequazione devo individuare per quali valori di x la funzione disegnata in blu $|𝑥 − 2|$ sta al di sopra della funzione disegnata in rosso $|𝑥 − 6|$ e ciò si verifica per $x>4$, dove $x=4$ è il punto medio tra $x=2$ e $x=6$ e rappresenta il punto di intersezione tra le due rette.
Soluzione quesito 4 della Simulazione Maturità Scientifica dicembre 2019 Matematica
Detto L il lato del quadrato, la sua superficie è pari a
\({{S}_{quadrato}}={{L}^{2}}\)
Nel primo quadrato è contenuta la quarta parte della superficie di un cerchio
\({{S}_{Cerchio1}}=\frac{\pi {{R}^{2}}}{4}\)
Nel secondo quadrato è contenuta la superficie di un cerchio
\({{S}_{Cerchio2}}=\pi {{r}^{2}}\)
Come indicato nella traccia si ha che
\({{S}_{Cerchio1}}={{S}_{Cerchio1}}=\frac{1}{2}{{S}_{quadrato}}\)\(\Rightarrow \)\(\pi {{r}^{2}}=\frac{\pi {{R}^{2}}}{4}\)\(\Rightarrow \)\(\frac{R}{r}=2\)
Soluzione quesito 5 della Simulazione Maturità Scientifica dicembre 2019 Matematica
Traccia un’altra parallela $DE$, passante per due punti $D$ ed $E$ appartenenti alla parabola, e mostra che i punti medi delle tre parallele giacciono su una retta.
La retta passante per O e C ha equazione \(y=mx\), con \(m=\frac{\Delta y}{\Delta x}=\frac{{{c}^{2}}}{c}=c\)
La retta passante per A e B ha lo stesso coefficiente angolare ma equazione \(y=mx+q\)
Dove l’intercetta q può essere calcolata imponendo il passaggio da A.
\(y=cx+q\)\(\Rightarrow \)\({{a}^{2}}=ca+q\)\(\Rightarrow\)\(y=cx+{{a}^{2}}-ca\)
La seconda retta interseca la parabola nel punto B=(b,b2), quindi si possono sostituire le coordinate del punto nell’equazione della retta.
\({{b}^{2}}=cb+{{a}^{2}}-ca\)\(\Rightarrow \)\({{b}^{2}}-{{a}^{2}}=cb-ca\)\(\Rightarrow\)\(\left( b-a \right)\left( b+a \right)=c\left( b-a \right)\)\(\Rightarrow \)\(b+a=c\)
La retta DE ha ancora lo stesso coefficiente angolare \(m=c\). Inoltre tenuto conto dell’equazione dimostrata al punto precedente \(b+a=c\), la stessa relazione vale per la retta DE con equazione \(d+e=c\)
Il punto medio di AB ha coordinate \({{M}_{AB}}=\left( \frac{a+b}{2},\frac{a{}^{2}+{{b}^{2}}}{2} \right)=\left( \frac{c}{2},\frac{a{}^{2}+{{b}^{2}}}{2} \right)\)
Il punto medio di DE ha coordinate \({{M}_{DE}}=\left( \frac{c}{2},\frac{d{}^{2}+{{e}^{2}}}{2} \right)\)
Il punto medio di OC ha coordinate \({{M}_{OC}}=\left( \frac{c}{2},\frac{{{c}^{2}}}{2} \right)\)
Le coordinate dei tre punti medi hanno in comune il valore dell’ascissa, pertanto si trovano tutti su una retta verticale di equazione x=c/2.
Soluzione quesito 6 della Simulazione Maturità Scientifica dicembre 2019 Matematica
Una funzione polinomiale cubica ha equazione \(y=f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d\)
Per individuare le coordinate del punto di flesso, bisogna studiare il segno della derivata seconda.
\({f}'(x)=3a{{x}^{2}}+2bx+c\)
\({f}”(x)=6ax+2b>0\)\(\Rightarrow\)\(x>-\frac{b}{3a}\)
Il flesso si ha in xF=-b/(3a)
Interseca l’asse x nei punti di ascissa 10, 100 e 1000, vuol dire che passa per i punti A=(10,0), B=(100,0), C=(1000,0). Si ottiene il sistema
Interseca l’asse x nei punti di ascissa 10, 100 e 1000, vuol dire che passa per i punti A=(10,0), B=(100,0), C=(1000,0). Si ottiene il sistema
$$\left\{\begin{align*}& 10^3a + 10^2b + 10c + d = 0 \\& 100^3a + 100^2b + 100c + d = 0 \\& 1000^3a + 1000^2b + 1000c + d = 0\end{align*}\right.$$
Divido tutte le equazioni del sistema per $a$, e chiamo $b’ = \frac{b}{a}$, $c’ = \frac{c}{a}$ e $d’ = \frac{d}{a}$.
$$\left\{\begin{align*}& 10^2b’ + 10c’ + d’ = -10^3 \\& 100^2b’ + 100c’ + d’ = -100^3 \\& 1000^2b’ + 1000c’ + d’ = -1000^3\end{align*}\right.$$
A questo punto ho ottenuto un sistema a 3 equazioni e 3 incognite, dal quale sono interessato a calcolare la variabile b’ che posso ottenerla attraverso il metodo di Cramer.
\({b}’=\frac{\det \left| \begin{matrix} -{{10}^{3}} & 10 & 1 \\ -{{100}^{3}} & 100 & 1 \\ -{{1000}^{3}} & 1000 & 1 \\ \end{matrix} \right|}{\det \left| \begin{matrix} {{10}^{2}} & 10 & 1 \\ {{100}^{2}} & 100 & 1 \\ {{1000}^{2}} & 1000 & 1 \\ \end{matrix} \right|}=-1110\)
A questo punto, noto b’, posso calcolare la coordinata x del flesso e vale
\({{x}_{F}}=-\frac{b}{3a}=-\frac{{{b}’}}{3}=\frac{1110}{3}\)
La funzione f(x) può essere riscritta nella forma $f(x)=a(x-10)(x-100)(x-1000)$, considerato che ha tre zeri in corrispondenza di 10, 100 e 1000.
A questo punto la coordinata $y_F$ del punto di flesso si ottiene sostituendo nell’equazione la coordinata
$$ y_F = a(x_F – 10)(x_F – 100)(x_F – 1000) $$
Concludiamo dicendo che la coordinata x del punto di flesso può essere determinata numericamente, mentre la coordinata y dipende dal parametro a e pertanto non può essere determinata in maniera univoca. Il tutto può essere giustificato da un punto di vista geometrico considerando che per tre punti distinti del piano cartesiano, se il sistema ottenuto imponendo il passaggio dai 3 punti ammette soluzione, passano infinite funzioni polinomiali (fascio di curve).
Soluzione quesito 7 della Simulazione Maturità Scientifica dicembre 2019 Matematica
Il raggio della sfera è pari alla distanza tra il centro e il piano
\(R={{d}_{K\Pi }}=\frac{\left| a{{x}_{P}}+b{{y}_{P}}+c{{z}_{P}}+d \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}=\frac{\left| 1\cdot 1-2\cdot 0+1\cdot 1+1 \right|}{\sqrt{1+4+1}}=\frac{3}{\sqrt{6}}=\sqrt{\frac{3}{2}}\)
Dove abbiamo usato la formula della distanza tra un punto e una retta nello spazio
\(d=\frac{\left| a{{x}_{P}}+b{{y}_{P}}+c{{z}_{P}}+d \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\)
Dove \(ax+by+cz+d=0\) è l’equazione del piano, mentre \(\left( {{x}_{P}},{{y}_{P}},{{z}_{P}} \right)\) rappresentano le coordinate del punto.
Soluzione quesito 8 della Simulazione Maturità Scientifica dicembre 2019 Matematica
La probabilità p di ottenere su quattro lanci due teste e due croci, in qualsiasi ordine, è data dal rapporto tra il numero di casi favorevoli f e il numero di casi possibili u. Il numero dei casi favorevoli f è dato dal numero di modi in cui possono uscire due teste e due croci lanciando quattro volte una moneta.
Utilizzando le permutazioni semplici di quattro elementi, a due a due ripetuti, otteniamo:
\(f=P_{4}^{(2,2)}=\frac{4!}{2!2!}=6\)
Il numero dei casi possibili è u=24 perché in ogni lancio ci sono due possibili esiti.
Pertanto \(p=\frac{f}{4}=\frac{6}{{{2}^{4}}}=0.375=37.5\%\) che è minore del $50\%$.
