14 Esercizi svolti su integrali tripli

$\iiint\limits_{A}{\frac{y}{{{z}^{4}}+1}dxdydz}$ , $A=\{ (x,y,z)\in {{\mathbb{R}}^{3}}:\,\,\,0\le z\le 1,\,\,\,\,{{x}^{2}}+{{y}^{2}}\le {{z}^{2}},\,\,\,\,z\le x+y \}$

Vedremo nella soluzione che l’insieme A infatti rappresenta il volume compreso tra un cono e un piano. Il piano interseca il cono e il vertice del cono è tagliato dal piano. Continua a leggere per vedere la soluzione anche se ti consiglio di provare prima a svolgerlo da solo. Ti anticipo che il risultato atteso è $\frac{\ln{2}}{24}$. Tutti i risultati in questo sito sono esatti, perché svolti e controllati con l’aiuto di professori di Analisi Matematica dell’università di Pisa.

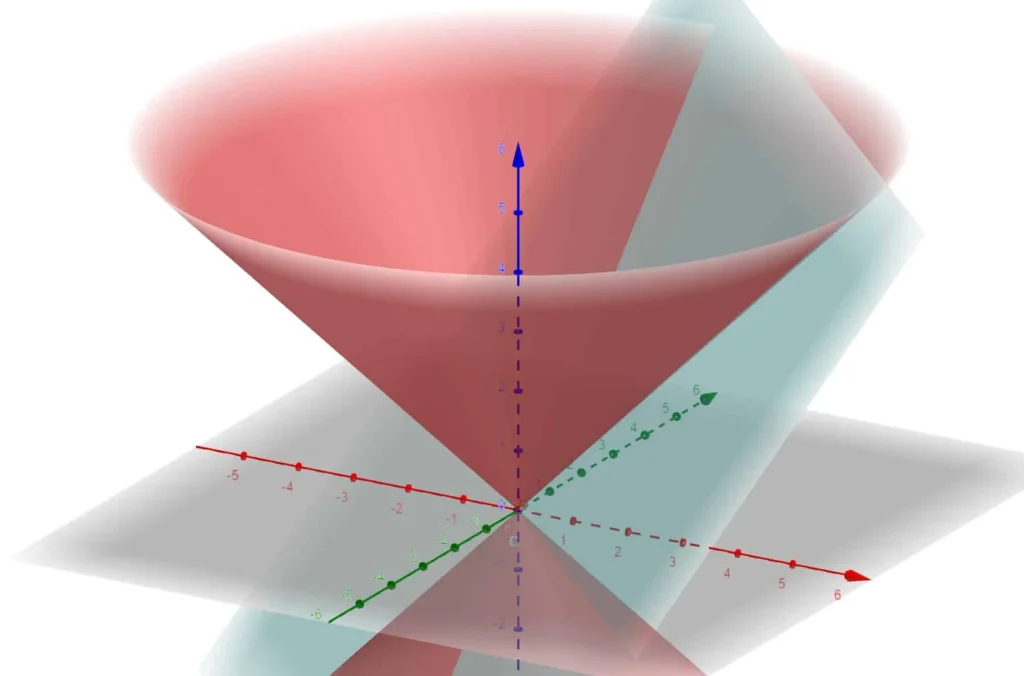
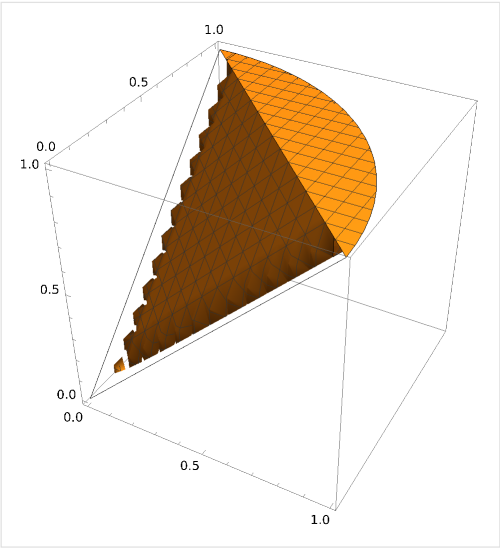
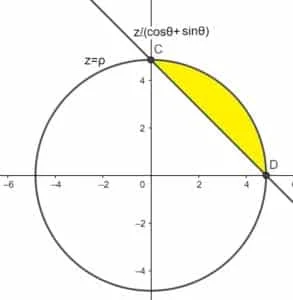
Per prima cosa proviamo a capire di cosa si tratta l’insieme di integrazione.

$0\le z\le 1$ rappresenta la parte di spazio compresa tra i piani z=0 e z=1.

${{x}^{2}}+{{y}^{2}}={{z}^{2}}$ rappresenta l’equazione di un cono e il minore o uguale sta ad indicare che bisogna prendere la parte interna.

Nel grafico è rappresentato il grafico tridimensionale dell’insieme A su cui dobbiamo integrare la funzione. L’insieme A è costituito dalla parte di spazio compresa tra il piano e il cono.

Il secondo grafico mostra invece una sezione del solido a z fissato

Considerando che la sezione del solido che si ottiene tagliando il grafico a una certa quota z con $0\le z\le 1$ è una circonferenza di raggio z tagliata da una retta.

L’insieme può essere ben rappresentato in coordinate polari.

Ponendo quindi $x=\rho \cos \theta $ e $y=\rho \sin \theta $ , si ha:

$0\le z\le 1$  resta invariato.

${{x}^{2}}+{{y}^{2}}\le {{z}^{2}}$ $\rightarrow $ ${{( \rho \cos \theta  )}^{2}}+{{( \rho \sin \theta  )}^{2}}\le {{z}^{2}}$ $\rightarrow $ ${{\rho }^{2}}\le {{z}^{2}}$ $\rightarrow $ $\rho \le z$

$z\le x+y$ $\rightarrow $ $z\le \rho \cos \theta +\rho \sin \theta $ $\rightarrow $ $\rho \ge \frac{z}{\cos \theta +\sin \theta }$.

L’insieme descritto in coordinate polari diventa:

${A}’=\{ (\rho ,\theta ,z)\in {{\mathbb{R}}^{3}}:\,\,\,0\le z\le 1,\,\,0\le \theta \le \frac{\pi }{2},\,\,\,\,\frac{z}{\cos \theta +\sin \theta }\le \rho \le z,\,\,\,\, \}$

L’insieme A descritto in coordinate polari diventa normale rispetto a z e rispetto a θ. Nel passare in coordinate polari bisogna ricordarsi di moltiplicare la funzione per il modulo del determinante della matrice Jacobiana che nel caso di coordinate polari vale $| \det \mathbf{J} |=\rho $ .

$\iiint\limits_{A}{f(x,y,z)dxdydz}=$ $\iiint\limits_{{{A}’}}{f(\rho \cos \theta ,\rho \sin \theta ,z)\cdot \rho \cdot d\rho d\theta dz}=$ $\int\limits_{\theta =0}^{\frac{\pi }{2}}{\int\limits_{z=0}^{1}{\int\limits_{\rho =\frac{z}{\cos \theta +\sin \theta }}^{z}{\frac{\rho \sin \theta }{{{z}^{4}}+1}}}\cdot \rho \cdot d\rho \cdot d\theta \cdot dz}=$

$\int\limits_{\theta =0}^{\frac{\pi }{2}}{\sin \theta [ \int\limits_{z=0}^{1}{\frac{1}{{{z}^{4}}+1}( \int\limits_{\rho =\frac{z}{\cos \theta +\sin \theta }}^{z}{{{\rho }^{2}}\cdot d\rho } )dz} ]d\theta }=$

$\int\limits_{\theta =0}^{\frac{\pi }{2}}{\sin \theta [ \int\limits_{z=0}^{1}{\frac{1}{{{z}^{4}}+1} [ \frac{{{\rho }^{3}}}{3}]_{\frac{z}{\cos \theta +\sin \theta }}^{z}dz} ]}d\theta =$

$\int\limits_{\theta =0}^{\frac{\pi }{2}}{\sin \theta [ \int\limits_{z=0}^{1}{\frac{1}{{{z}^{4}}+1} [ \frac{{{z}^{3}}}{3}-\frac{1}{3} ( \frac{z}{\cos \theta +\sin \theta } )^{3} ]\cdot dz} ]}d\theta =$

$\int\limits_{\theta =0}^{\frac{\pi }{2}} (1 – \frac{1}{(\cos \theta + \sin \theta)^{3}} ) \sin \theta [ \frac{1}{3} \int\limits_{z=0}^{1} \frac{z^{3}}{z^{4} + 1} \cdot dz ] \cdot d\theta =$

A questo punto abbiamo ottenuto un integrale doppio a variabili separabili e quindi possiamo scriverlo come il prodotto di due integrali separati:

$\int\limits_{\theta =0}^{\frac{\pi }{2}}{( 1-\frac{1}{{{( \cos \theta +\sin \theta )}^{3}}} )\sin \theta \,}d\theta \cdot \frac{1}{3}\int\limits_{z=0}^{1}{\frac{{{z}^{3}}}{{{z}^{4}}+1}\cdot dz}=$

A questo punto risolviamo singolarmente i due integrali. Partiamo dal risolvere il primo:

$\frac{1}{3}\int\limits_{0}^{1}{\frac{{{z}^{3}}}{{{z}^{4}}+1}\cdot dz}=$ $\frac{1}{12}\int\limits_{0}^{1}{\frac{4{{z}^{3}}}{{{z}^{4}}+1}dz}=$ $\frac{1}{12}[ \ln ( {{z}^{4}}+1 ) ]_{0}^{1}=\frac{1}{12}\ln 2$

Risolviamo il secondo:

$\int\limits_{0}^{\frac{\pi }{2}}{( 1-\frac{1}{{{( \cos \theta +\sin \theta )}^{3}}} )\sin \theta \,}d\theta$

$=\int\limits_{0}^{\frac{\pi }{2}}{\sin \theta d\theta }-\int\limits_{0}^{\frac{\pi }{2}}{\frac{\sin \theta }{{{( \cos \theta +\sin \theta )}^{3}}}d\theta }=$

Abbiamo da calcolare la somma di due integrali e risolviamoli singolarmente, il primo è immediato:

$\int\limits_{0}^{\frac{\pi }{2}}{\sin \theta d\theta }=$ $[ -\cos \theta  ]_{0}^{\pi /2}=1$

Per quanto riguarda il secondo dividiamo numeratore e denominatore per ${{\cos }^{3}}\theta $, e otteniamo una espressione con $\tan \theta $:

$\int\limits_{\theta =0}^{\frac{\pi }{2}} \frac{\frac{\sin \theta}{{\cos}^3 \theta}}{{\left(1 + \frac{\sin \theta}{\cos \theta}\right)}^3} d\theta =$

$\int\limits_{\theta =0}^{\frac{\pi }{2}} \frac{\frac{\sin \theta}{\cos \theta}}{{\left(1 + \frac{\sin \theta}{\cos \theta}\right)}^3} \frac{1}{{\cos}^2 \theta} d\theta =$

$\int\limits_{\theta =0}^{\frac{\pi }{2}} \frac{\tan \theta}{{\left(1 + \tan \theta\right)}^3} \frac{1}{{\cos}^2 \theta} d\theta =$

Riconoscendo che $\frac{1}{{{\cos }^{2}}\theta }$ è la derivata della tangente possiamo fare la sostituzione $\tan \theta =x$ $\Rightarrow $ $\frac{1}{{{\cos }^{2}}\theta }d\theta =dx$ e sostituendo nell’integrale si ha:

Ecco la formula corretta in formato LaTeX:

$\int\limits_{0}^{+\infty} \frac{x}{{(1+x)^3}}dx =$

$\int\limits_{0}^{+\infty} \frac{x+1-1}{{(1+x)^3}}dx =$

$\int\limits_{0}^{+\infty} \frac{x+1}{{(1+x)^3}} – \frac{1}{{(1+x)^3}}dx =$

$\int\limits_{0}^{+\infty} (x+1)^{-2} – (x+1)^{-3}dx =$

$\left[-\frac{1}{x+1} + \frac{1}{2(x+1)^2}\right]_{0}^{+\infty} = \frac{1}{2}$

Possiamo pertanto concludere che:

$\iiint\limits_{A}{\frac{y}{{{z}^{4}}+1}dxdydz}=$ $\frac{\ln 2}{12}( 1-\frac{1}{2} )=\frac{\ln 2}{24}$