Indice dei contenuti
In questa pagina vedremo insieme lo svolgimento di esercizi limiti in coordinate polari.
Per risolvere i limiti di due variabili utilizzando le coordinate polari, è importante comprendere il concetto di coordinate polari e come applicarle in situazioni di calcolo.
Le coordinate polari sono un sistema di coordinate che rappresenta un punto nel piano attraverso la distanza radiale dal punto all’origine e l’angolo che il raggio vettore forma con l’asse x positivo.
Questo sistema di coordinate è particolarmente utile quando si tratta di risolvere problemi che coinvolgono simmetria circolare o forme circolari.
Per risolvere un limite di due variabili utilizzando le coordinate polari, è necessario trasformare le variabili x e y in variabili r e θ. Questo viene fatto utilizzando le seguenti relazioni: x = r * cos(θ) y = r * sin(θ).
Una volta che le variabili sono state trasformate, è possibile riscrivere l’espressione del limite utilizzando r e θ anziché x e y. Questo può semplificare notevolmente il calcolo del limite e rendere più chiara la soluzione.
Un esempio di come risolvere un limite di due variabili utilizzando le coordinate polari potrebbe essere il seguente: supponiamo di dover calcolare il limite di una funzione f(x, y) quando x e y si avvicinano a zero. Utilizzando le coordinate polari, possiamo trasformare le variabili x e y in r e θ e riscrivere la funzione f(r, θ).
Questo ci permette di valutare il limite in modo più semplice e preciso, tenendo conto della simmetria circolare della funzione. In conclusione, l’utilizzo delle coordinate polari per risolvere i limiti di due variabili può semplificare notevolmente il calcolo e portare a soluzioni più chiare e concise.
È importante comprendere come applicare correttamente le coordinate polari e come trasformare le variabili x e y in r e θ per ottenere risultati accurati e significativi e in questa pagina vedremo proprio questo: Alcuni esercizi svolti in coordinate polari
Risolvere limiti in due variabili con le coordinate polari
Vediamo come risolvere limiti in due variabili con l’ausilio di coordinate polari.
Vogliamo calcolare i seguenti limiti:
1) $\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{\lim }}\,\frac{x{{y}^{2}}}{{{x}^{2}}+{{y}^{2}}}$
2) $\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{\lim }}\,\frac{xy}{{{x}^{2}}+{{y}^{2}}}$
3) $\underset{\left( x,y \right)\to \left( -1,2 \right)}{\mathop{\lim }}\,\frac{\left( x+1 \right){{\left( y-2 \right)}^{2}}}{{{x}^{2}}+{{y}^{2}}-4y+2x+5}$
In questa lezione impariamo a risolvere limiti in due variabili con l’ausilio di coordinate polari.
1. Soluzione del primo limite
$\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{\lim }}\,\frac{x{{y}^{2}}}{{{x}^{2}}+{{y}^{2}}}$
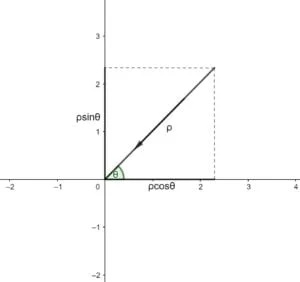
Per prima cosa definiamo le coordinate polari come il cambio di variabili $\left( x,y \right)=\left( \rho \cos \theta ,\rho \sin \theta \right)$, con $\theta \in \left[ 0,2\pi \right]$e $\rho \ge 0$ . Per ogni valore di $\theta $, cambia la direzione del vettore che tende a zero. Naturalmente per $(x,y)\to (0,0)$ si ha che $\rho \to {{0}^{+}}$.
Nel grafico è rappresentato il significato geometrico delle coordinate polari.
Il limite esiste, se il risultato non dipende da θ. Facciamo la sostituzione nella funzione e si ha:
$\frac{x{{y}^{2}}}{{{x}^{2}}+{{y}^{2}}}$
$=\frac{\rho \cos \theta \cdot {{\rho }^{2}}\,{{\sin }^{2}}\theta }{{{\rho }^{2}}\,{{\cos }^{2}}\theta +{{\rho }^{2}}\,{{\sin }^{2}}\theta }$
$=\frac{\rho \cos \theta \cdot \,{{\sin }^{2}}\theta }{\,{{\cos }^{2}}\theta +\,{{\sin }^{2}}\theta } \text{ con } \theta \in \left[ 0,2\pi \right]$
A questo punto considerando che seno e coseno sono entrambi quantità limitate tra -1 e 1, anche il loro prodotto sarà limitato tra le stesse quantità e possiamo quindi scrivere la disuguaglianza:
$\left| \rho \cos \theta \,{{\sin }^{2}}\theta \right|<\rho $
Inoltre considerato che se $\left( x,y \right)\to (0,0)$ $\Rightarrow $ $\rho \to {{0}^{+}}$, possiamo portare la disuguaglianza al limite e si ha:
$\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{\lim }}\,\left| \frac{x{{y}^{2}}}{{{x}^{2}}+{{y}^{2}}} \right|\le \underset{\rho \to {{0}^{+}}}{\mathop{\lim }}\,\rho =0$
A questo punto per il teorema del confronto possiamo concludere che poiché la funzione per $(x,y)\to (0,0)$ è minore di una quantità che tende a zero, allora il limite della funzione $\frac{x{{y}^{2}}}{{{x}^{2}}+{{y}^{2}}}$ tende anche esso a zero.
$\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{\lim }}\,\frac{x{{y}^{2}}}{{{x}^{2}}+{{y}^{2}}}=0$
2. Soluzione del secondo limite
Andiamo a risolvere il secondo limite:
$\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{\lim }}\,\frac{xy}{{{x}^{2}}+{{y}^{2}}}$
Sostituiamo di nuovo nel limite le coordinate polari $\left( x,y \right)=\left( \rho \cos \theta ,\rho \sin \theta \right)$ come nell’esercizio precedente e si ha facendo passaggi simili al caso precedente:
$\underset{\left( x,y \right)\to (0,0)}{\mathop{\lim }}\,\frac{xy}{{{x}^{2}}+{{y}^{2}}}$
$=\underset{\rho \to {{0}^{+}}}{\mathop{\lim }}\,\frac{\rho \cos \theta \cdot \rho \,\sin \theta }{{{\rho }^{2}}\,{{\cos }^{2}}\theta +{{\rho }^{2}}\,{{\sin }^{2}}\theta }$
$=\underset{\rho \to {{0}^{+}}}{\mathop{\lim }}\,\frac{\cos \theta \cdot \,\sin \theta }{\,{{\cos }^{2}}\theta +\,{{\sin }^{2}}\theta }$
$=\cos \theta \cdot \,\sin \theta \text{ con } \theta \in \left[ 0,2\pi \right]$
Il risultato dipende da θ e possiamo pertanto concludere che il limite non esiste. Infatti il limite esiste se il risultato non dipende da θ e quindi dalla direzione con cui $(x,y)\to (0,0)$
3. Soluzione del terzo limite
Vediamo come risolvere limiti in due variabili con l’ausilio di coordinate polari, anche in un caso non del tutto immediato come questo.
$\underset{\left( x,y \right)\to \left( -1,2 \right)}{\mathop{\lim }}\,\frac{\left( x+1 \right){{\left( y-2 \right)}^{2}}}{{{x}^{2}}+{{y}^{2}}-4y+2x+5}$
Per cominciare osserviamo che in questo caso con $(x,y)\to (-1,2)$ , si ha che $(x+1)\to 0$ e che $(y-2)\to 0$.
In questo caso andiamo ad usare le coordinate polari traslate, ovvero centrate in $(-1,2)$. Per fare ciò scriviamo $(x,y)=(\rho \cos \theta -1,\rho \sin \theta +2)$ con $\rho \to {{0}^{+}}$ e $\theta \in \left[ 0,2\pi \right]$.
Riscriviamo il denominatore della funzione completando i quadrati e si ha:
$\frac{\left( x+1 \right){{\left( y-2 \right)}^{2}}}{{{x}^{2}}+{{y}^{2}}-4y+2x+5}$
$=\frac{\left( x+1 \right){{\left( y-2 \right)}^{2}}}{{{x}^{2}}+{{y}^{2}}-4y+2x+4+1}$
$ \frac{(x+1)(y-2)^2}{(x+1)^2 + (y-2)^2} $
A questo punto facciamo la sostituzione $(x,y)=(\rho \cos \theta -1,\rho \sin \theta +2)$ e si ha:
$ \frac{(\rho \cos \theta+1 -1)(\rho \sin \theta +2-2)^2}{(\rho \cos \theta +1 -1)^2 + (\rho \sin \theta +2-2)^2} $
$=\rho \cos \theta {{\sin }^{2}}\theta $
Come per il primo caso possiamo scrivere la disuguaglianza:
$\underset{\left( x,y \right)\to \left( -1,2 \right)}{\mathop{\lim }}\,\frac{\left( x+1 \right){{\left( y-2 \right)}^{2}}}{{{x}^{2}}+{{y}^{2}}-4y+2x+5}\le\underset{\left( x,y \right)\to \left( -1,2 \right)}{\mathop{\lim }}\,\left| \frac{\left( x+1 \right){{\left( y-2 \right)}^{2}}}{{{x}^{2}}+{{y}^{2}}-4y+2x+5} \right|\le \underset{\rho \to {{0}^{+}}}{\mathop{\lim }}\,\rho =0$
Anche in questo caso per il teorema del confronto, si ha che il risultato del limite è zero.
Abbiamo appena visto come risolvere limiti in due variabili con l’ausilio di coordinate polari, continua la navigazione per leggere altri esempi e lezioni.
